Operaciones con Conjuntos

Las operaciones con conjuntos incluyen la unión, la intersección y la diferencia.

Para explicar de forma clara las operaciones con conjuntos, esta página recurre principalmente a diagramas de Venn, ya que permiten visualizar mejor estos conceptos. La representación gráfica suele ser mucho más intuitiva que la notación matemática.

Unión

Dado dos conjuntos A y B, la unión de A y B es el conjunto formado por todos los elementos que pertenecen a A, a B o a ambos.

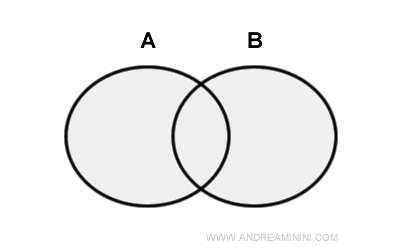
El símbolo que representa la unión es ∪.

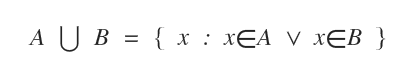
En la unión, los elementos que aparecen en ambos conjuntos se cuentan una sola vez.

Unión de múltiples conjuntos. Para expresar la unión de una familia de conjuntos, se puede escribir así: $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{para algún}\:\: i \in I \} $$

Cómo calcular la unión de dos conjuntos

Veamos un ejemplo práctico del cálculo de la unión de dos conjuntos A y B.

Explicación. El conjunto A contiene los elementos { 2, 5, 6, 7, 8 }, mientras que el conjunto B está formado por { 1, 3, 4, 6, 7, 9 }. La unión de ambos conjuntos es { 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Los elementos en común {6, 7} solo se incluyen una vez.

Intersección

La intersección de dos conjuntos A y B es el conjunto de los elementos que son comunes a ambos.

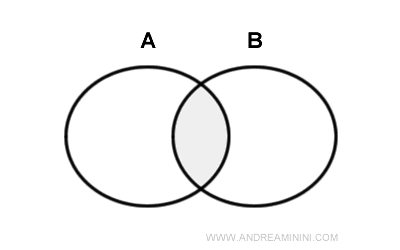
El símbolo de la intersección es ⋂.

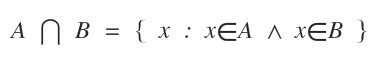
Dos conjuntos A y B son disjuntos si su intersección A⋂B es el conjunto vacío.

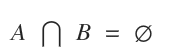
Intersección de múltiples conjuntos. La intersección de una familia de conjuntos se expresa como: $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Cómo calcular la intersección de dos conjuntos

A continuación, un ejemplo práctico de intersección de conjuntos.

Explicación. Los elementos { 6, 7 } están presentes en ambos conjuntos, por lo que la intersección A⋂B es { 6, 7 }.

Diferencia entre conjuntos

La diferencia entre dos conjuntos A y B, denotada como A - B, es el conjunto de los elementos que están en A pero no en B.

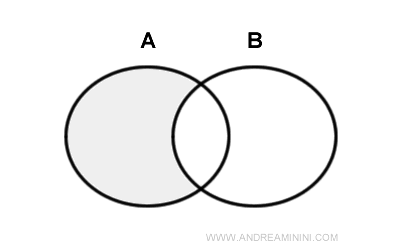
También se conoce como el complemento de B respecto a A.

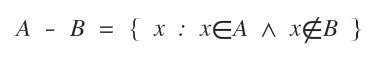
Nota. La diferencia A - B también se llama complemento relativo de A en B. Contiene todos los elementos de A que no están en B. Se expresa como: $$ A \text{ \ } B =\{ x \in A | x \notin B \} $$

Cómo calcular la diferencia entre dos conjuntos

Ejemplo práctico del cálculo de la diferencia entre A y B.

Explicación. El conjunto A contiene los elementos {2, 5, 6, 7, 8}. Como los elementos {6, 7} están en ambos conjuntos, se eliminan al calcular A - B, resultando en {2, 5, 8}.

Propiedades de las Operaciones con Conjuntos

Las operaciones con conjuntos cumplen con las siguientes propiedades fundamentales: conmutativa, asociativa, distributiva y las leyes de De Morgan.

• Propiedad conmutativa

  A ∪ B = B ∪ A
  A ∩ B = B ∩ A

• Propiedad asociativa

  A ∪ (B ∪ C) = (A ∪ B) ∪ C
  A ∩ (B ∩ C) = (A ∩ B) ∩ C

• Propiedad distributiva

  A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
  A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

• Leyes de De Morgan

  A - (B ∪ C) = (A - B) ∩ (A - C)
  A - (B ∩ C) = (A - B) ∪ (A - C)