Subconjuntos Impropios
¿Qué son los subconjuntos impropios?
Los subconjuntos impropios se definen como aquellos que son iguales al conjunto mismo o al conjunto vacío.
Todo conjunto A siempre tiene dos subconjuntos impropios:
- el conjunto idéntico a sí mismo $$ A = A $$
- el conjunto vacío $$ Ø ⊂ A $$
Conjuntos Iguales
Supongamos que tenemos dos conjuntos iguales (A = B).
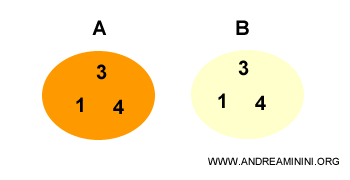
Cada elemento del conjunto A también está en el conjunto B.
Por lo tanto, A es un subconjunto de B:
$$ A ⊆ B $$
De la misma manera, cada elemento de B también está en A.
Por lo tanto, B es un subconjunto de A:
$$ B ⊆ A $$
Esta relación recíproca implica que ambos conjuntos son idénticos.
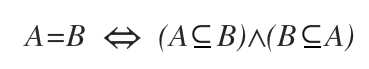
Por lo tanto, cuando dos conjuntos son iguales (A = B), cada uno es subconjunto del otro.
En estos casos, hablamos de subconjuntos impropios, ya que ni A ni B son subconjuntos propios uno del otro.
Nota. Un conjunto A es un subconjunto propio de B si todos los elementos de A están en B, pero hay al menos un elemento en B que no está en A. Esto no ocurre cuando los conjuntos son iguales.
Ejemplo
El conjunto A está contenido en B y viceversa:
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4 \} $$
Cada elemento de A también está en B y cada elemento de B también está en A.
Por lo tanto, estos dos conjuntos son subconjuntos impropios entre sí.
El Conjunto Vacío
Un conjunto se llama conjunto vacío cuando no contiene ningún elemento.
Se representa con el símbolo Ø: $$ Ø = \{ \ \ \} $$
El conjunto vacío es un subconjunto impropio de cualquier otro conjunto.
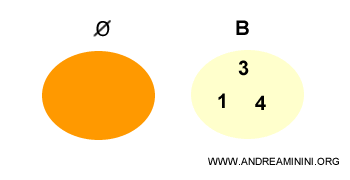
Nota. El hecho de que el conjunto vacío sea un subconjunto de cualquier conjunto puede parecer contraintuitivo, pero es demostrable (ver demostración). A continuación, trataré de explicarlo.
Ejemplo
Consideremos el conjunto vacío y un conjunto A cualquiera:
$$ Ø = \{ \ \ \} $$
$$ A = \{ 1,3,4 \} $$
El conjunto vacío Ø está contenido en A:
$$ Ø ⊂ A $$
Para demostrarlo, supongamos lo contrario e intentemos llegar a una contradicción.
"El conjunto vacío NO es un subconjunto de A"
Si esto fuera cierto, debería haber al menos un elemento en el conjunto vacío que no esté en A.
Pero esto es imposible, porque el conjunto vacío no tiene elementos.
Por lo tanto, la afirmación "El conjunto vacío NO es un subconjunto de A" es falsa.
Si esta afirmación es falsa, su opuesta "El conjunto vacío ES un subconjunto de A" debe ser verdadera.
Demostración Alternativa. La unión de un conjunto A con cualquiera de sus subconjuntos B⊆A da como resultado el mismo conjunto A: $$ A \cup B = A $$ Esto también se cumple con el conjunto vacío: $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$