Diferencia entre Conjuntos
La diferencia entre dos conjuntos A y B es un conjunto (llamado conjunto diferencia) que contiene los elementos de A que no pertenecen a B. $$ A-B = \{ x \ | \ x \ \in A \ ∧ \ x \notin \ B \} $$ Se lee como "A menos B". A continuación, se muestra el diagrama de Venn.
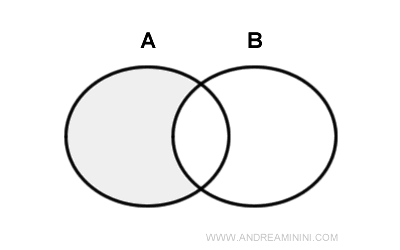
En algunos casos, la diferencia entre conjuntos también se representa de la siguiente manera:
$$ A \text{ \ } B $$
Se interpreta como "el conjunto A\B es el complemento del conjunto B".
Ejemplo Práctico
Supongamos que tenemos dos conjuntos finitos A y B:
$$ A = \{ 0, 2, 4, 8, 10 \} $$
$$ B = \{ 2, 4, 6, 12 \} $$
La diferencia entre ambos conjuntos es el conjunto A-B, que incluye los elementos de A que no están en B:
$$ A-B = A \text{ \ } B = \{ 0, 8, 10 \} $$
El conjunto diferencia está formado por los elementos de A que no aparecen en B, es decir, { 0, 8, 10}.
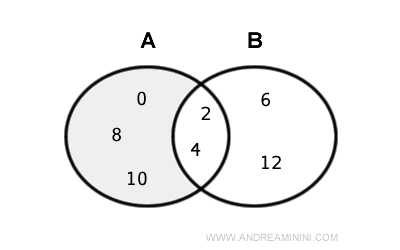
Los elementos comunes a ambos conjuntos, en este caso 2 y 4, se eliminan del conjunto diferencia.
Ejemplo 2
Veamos otro caso con los siguientes conjuntos finitos A y B:
$$ A = \{ 1, 2, 3, 4, 5, 6, 7 \} $$
$$ B = \{ 2, 4, 6 \} $$
Aquí, el conjunto B es un subconjunto propio de A.
La diferencia A-B es el conjunto que contiene los elementos de A que no están en B:
$$ A-B = A \text{ \ } B = \{ 1, 3, 5, 7 \} $$
El conjunto diferencia está compuesto por los elementos { 1, 3, 5, 7}.
En la representación mediante diagramas de Euler-Venn, el conjunto diferencia se muestra resaltado en gris.
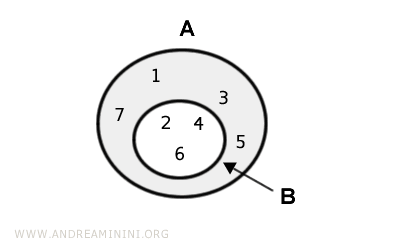
Propiedades de la Diferencia
A continuación, algunas propiedades clave de la diferencia entre conjuntos:
- La diferencia entre conjuntos no es conmutativa $$ A-B \ne B-A $$
Ejemplo. Consideremos los conjuntos $$ A = \{ 0, 2, 4, 8, 10 \} $$ $$ B = \{ 2, 4, 6, 12 \} $$ La diferencia A-B es $$ A-B = \{ 0, 8, 10 \} $$ mientras que la diferencia B-A es $$ B-A = \{ 6, 12 \} $$
- Si los conjuntos son disjuntos, la diferencia A-B es igual a A $$ A \cap B = Ø \Longleftrightarrow A-B= A $$
Ejemplo. Consideremos los conjuntos $$ A = \{ 2, 4, 6, 8 \} $$ $$ B = \{ 1, 3, 5, 7, 9 \} $$ La diferencia A-B es el propio conjunto A: $$ A-B = A = \{ 2, 4, 6, 8 \} $$ A continuación, se muestra la representación gráfica:
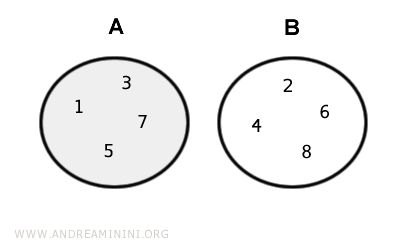
De manera similar, la diferencia B-A es igual a B: $$ B-A = B = \{ 1, 3, 5, 7,9 \} $$ - Si los conjuntos son iguales, la diferencia A-B es el conjunto vacío $$ A = B \Longleftrightarrow A-B= Ø $$
Estas propiedades pueden aplicarse a cualquier conjunto en operaciones de diferencia.