Colecciones de conjuntos
Una colección de conjuntos es un conjunto cuyos elementos son, a su vez, otros conjuntos.
En otras palabras, se trata de un conjunto formado por conjuntos.
Este concepto aparece en diversas ramas de las matemáticas, como la teoría de conjuntos, la topología y el álgebra abstracta.
¿Para qué sirve? Una colección de conjuntos permite definir estructuras matemáticas más complejas y analizar las relaciones entre distintos conjuntos.
A continuación, algunos ejemplos de colecciones de conjuntos:
- Familia de conjuntos
Se trata de una colección de conjuntos que comparten una propiedad común o cumplen ciertos criterios específicos. Un ejemplo típico es la familia de todos los conjuntos abiertos en un espacio topológico. - Partición de un conjunto
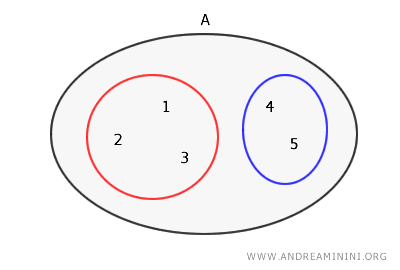
Una partición de un conjunto es una colección de conjuntos disjuntos cuya unión cubre completamente el conjunto original. Es decir, cada elemento del conjunto pertenece exactamente a uno de los conjuntos de la partición.Por ejemplo, dado el conjunto A={1,2,3,4,5}, una posible partición de A sería la colección formada por los subconjuntos { {1,2,3}, {4,5} }.
- Conjunto potencia (conjunto de todos los subconjuntos)
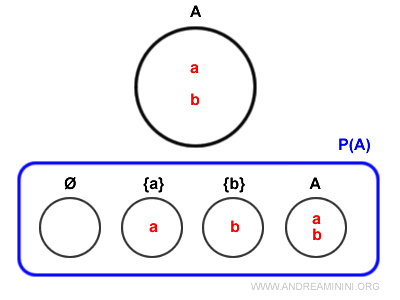
Es la colección que contiene todos los subconjuntos posibles de un conjunto dado, incluyendo tanto el conjunto vacío como el conjunto original.Por ejemplo, si tomamos el conjunto A={a,b}, su conjunto potencia P(A) está formado por los siguientes subconjuntos: { {}, {a}, {b}, {a,b} }.
Estos conceptos son fundamentales para el estudio de estructuras matemáticas más avanzadas y para explorar las relaciones y propiedades de los conjuntos en distintos contextos matemáticos.