Intersección de Conjuntos

La intersección de dos conjuntos A y B es el conjunto formado por todos los elementos que pertenecen tanto a A como a B.

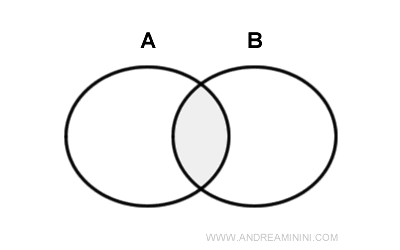
El símbolo de la intersección es ⋂.

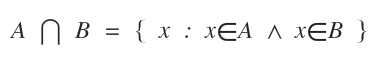
Esta notación se lee como "la intersección de A y B" o "A intersectado con B".

Intersección de múltiples conjuntos. Cuando se intersectan más de dos conjuntos, se puede usar esta notación más concisa para representar la intersección: $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Si dos conjuntos no tienen elementos en común, su intersección A⋂B es un conjunto vacío.

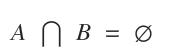
En este caso, los conjuntos se llaman conjuntos disjuntos.

Un Ejemplo Práctico

Supongamos que tenemos dos conjuntos finitos A y B:

$$ A = \{ 2,5,6,7, 8 \} $$

$$ B = \{ 1,3,4,6, 7,9 \} $$

Observamos que ambos conjuntos comparten dos elementos en común.

$$ A = \{ 2,5, \color{red}6,\color{red}7, 8 \} $$

$$ B = \{ 1,3,4,\color{red}6, \color{red}7,9 \} $$

Por lo tanto, la intersección de A y B está formada por los elementos 6 y 7.

$$ A \cap B = \{ 6,7 \} $$

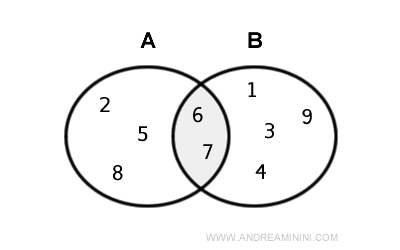
A continuación, se muestra la intersección representada mediante un diagrama de Euler-Venn.

 

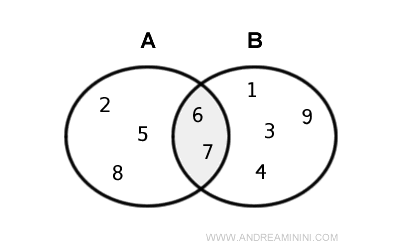
Tipos de Intersección

Dependiendo de la relación entre los conjuntos, su intersección puede tener diferentes características:

• La intersección A⋂B es un subconjunto propio de ambos conjuntos.

  Ejemplo. Dados los conjuntos $$ A = \{ 2,5,6,7, 8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ su intersección es $$ A \cap B = \{ 6,7 \} $$ En este caso, la intersección es un subconjunto propio de A y B: $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$ Este es el mismo ejemplo visto anteriormente.
  

• La intersección A⋂B es un subconjunto propio de uno de los conjuntos y un subconjunto impropio del otro. Esto sucede cuando uno de los conjuntos está contenido completamente dentro del otro, es decir, cuando A ⊆ B.

  Ejemplo. Dados los conjuntos $$ A = \{ 3,6,7 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ su intersección es $$ A \cap B = \{ 3, 6,7 \} $$ Gráficamente:
  
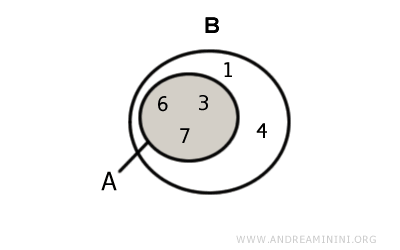
  En este caso, la intersección es un subconjunto impropio de A porque coincide exactamente con él: $$ A \cap B = A $$ mientras que es un subconjunto propio de B, ya que B contiene otros elementos que no pertenecen a A: $$ A \cap B ⊂ B $$

• La intersección A⋂B es un subconjunto impropio de ambos conjuntos. Esto ocurre en dos situaciones:
  
  A] Cuando los conjuntos son disjuntos, su intersección es el conjunto vacío, que es un subconjunto impropio de cualquier conjunto.
  

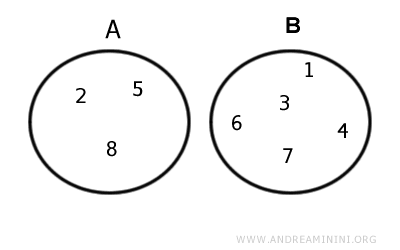
  Ejemplo. Dados los conjuntos $$ A = \{ 2,5,8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ su intersección es $$ A \cap B = \{ \ \ \} = Ø $$ En este caso, A y B no comparten ningún elemento.
  
  Dado que el conjunto vacío es un subconjunto impropio de cualquier conjunto, lo es también de A y B: $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$

  B] Cuando los conjuntos son idénticos. En este caso, su intersección es igual a ambos conjuntos.
  

  Ejemplo. Dados los conjuntos $$ A = \{ 1,2,3,4 \} $$ $$ B = \{ 1,2,3,4 \} $$ su intersección es igual a A y B: $$ A \cap B = A = B $$ En este caso, A y B contienen exactamente los mismos elementos, por lo que son conjuntos idénticos.
  
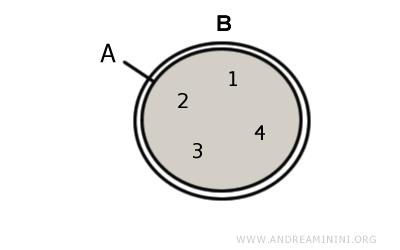
  Cuando dos conjuntos son iguales, son subconjuntos impropios el uno del otro.

Propiedades de la Intersección

La intersección de conjuntos cumple propiedades similares a las de la suma y la multiplicación de números.

• Propiedad conmutativa
  El orden de los conjuntos no afecta el resultado: $$ A \cap B = B \cap A $$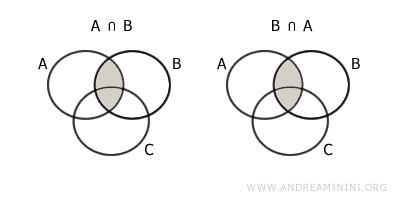

  

• Propiedad asociativa
  $$ (A \cap B) \cap C = A \cap (B \cap C) $$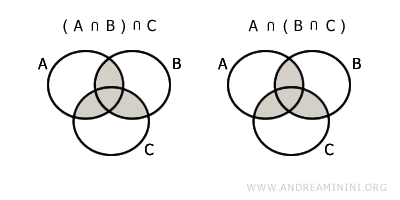

  

• Propiedad Distributiva con Respecto a la Unión
  $$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$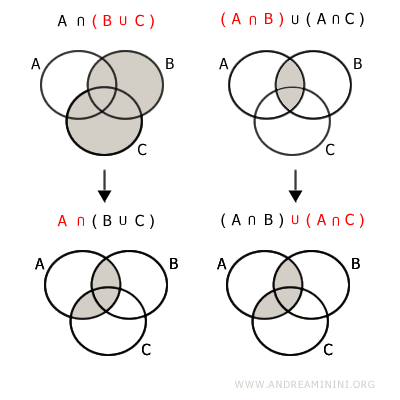

  

Y así sucesivamente.