Conjuntos ni abiertos ni cerrados
En topología, un conjunto que no es ni abierto ni cerrado no cumple con las condiciones para pertenecer a ninguna de estas dos categorías.
Este fenómeno puede darse en una topología donde el conjunto en cuestión no está definido como un conjunto abierto ni coincide con el complemento de uno.
Por lo tanto, dicho conjunto tampoco puede considerarse un conjunto cerrado.
Nota: En la topología usual de los números reales, visualizar conjuntos que no sean ni abiertos ni cerrados puede resultar poco intuitivo. No obstante, en estructuras topológicas más generales, su existencia es completamente natural. Un ejemplo concreto facilitará la comprensión de este concepto.
Ejemplo Práctico
Supongamos que tenemos el conjunto \( X = \{a,b,c,d\} \) y una topología \( T \) que define los siguientes conjuntos abiertos: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) y el conjunto vacío (Ø).
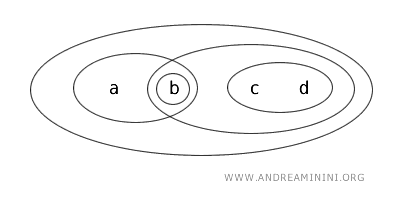
Analicemos ahora el subconjunto \( \{b,c\} \) de \( X \).
- El conjunto \( \{b,c\} \) no es abierto en la topología \( T \), ya que no aparece explícitamente en la lista de conjuntos abiertos.
- Asimismo, \( \{b,c\} \) tampoco es cerrado, porque su complemento \( X \setminus \{b,c\} = \{a,d\} \) no pertenece a la colección de conjuntos abiertos de \( T \).
En conclusión, en la topología \( T \), el conjunto \( \{b,c\} \) no es ni abierto ni cerrado.
Y así sucesivamente.