Clausura de un conjunto

La clausura de un conjunto \( A \) en un espacio topológico \( X \) es la intersección de todos los conjuntos cerrados que contienen a \( A \). Esta intersección se denota como \( \text{Cl}(A) \).

La clausura de A es el conjunto cerrado más pequeño que contiene a A en su totalidad.

No existe ningún conjunto cerrado que contenga a A y que sea estrictamente más pequeño que su clausura.

Nota: Esta propiedad se deduce directamente de la definición de clausura, ya que se construye como la intersección de todos los conjuntos cerrados que contienen a A. En esencia, la clausura es el conjunto cerrado más ajustado que puede contener a A: está formada por los elementos que aparecen en todos los conjuntos cerrados que contienen a A.

Formalmente, la clausura de A se expresa así:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ y } C \text{ es cerrado en } X \} $$

Aquí, \( \text{Cl}(A) \) representa la clausura de \( A \), y el símbolo \( \bigcap \) indica la intersección de todos los conjuntos cerrados \( C \) que contienen a \( A \).

La clausura de \( A \) incluye tanto los elementos del conjunto \( A \) como todos sus puntos límite dentro del espacio \( X \).

Nota: Es importante tener en cuenta que la clausura de un conjunto \( A \) está determinada, ante todo, por la topología del espacio \( X \) en el que se encuentra, y no tanto por las características propias de \( A \). Por ello, según la topología considerada, la clausura de \( A \) puede variar.

Un ejemplo ilustrativo

Consideremos el conjunto \( A = (0, 1) \) dentro de los números reales \( \mathbb{R} \), equipado con la topología estándar.

Se trata del intervalo abierto que contiene todos los números reales entre 0 y 1, excluyendo los extremos.

En este caso, la clausura de \( A \) es \( [0, 1] \).

$$ \text{Cl}(A) = [0,1] $$

Este conjunto incluye el intervalo abierto original \( (0,1) \) junto con sus puntos de acumulación en los extremos, es decir, los puntos 0 y 1.

Nota: En la topología estándar de \( \mathbb{R} \), un conjunto cerrado es aquel que contiene todos sus puntos límite. Un punto límite de un conjunto es aquel en cuya vecindad, por pequeña que sea, siempre hay al menos un punto del conjunto distinto de él. Por ejemplo, la intersección de los intervalos cerrados [0,2] y [-1,1] da como resultado el intervalo cerrado [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ No existe un intervalo cerrado más pequeño que contenga a (0,1).

Ejemplo 2

Veamos ahora el conjunto \( A = [0, 1) \) en \( \mathbb{R} \) con la topología estándar.

Este conjunto incluye todos los números reales desde 0, inclusive, hasta 1, sin incluir este último. Se trata, por tanto, de un intervalo cerrado por la izquierda y abierto por la derecha.

Una vez más, la clausura del conjunto es \( [0,1] \).

$$ \text{Cl}(A) = [0,1] $$

Esto ocurre porque el punto 0 ya pertenece al conjunto A, mientras que el punto 1 es un punto límite exterior.

Así, la clausura de A incorpora el extremo abierto derecho del intervalo, resultando en [0,1], el conjunto cerrado más pequeño que contiene a A.

Nota: Esto es coherente con el concepto de clausura en topología, el cual incluye todos los puntos de acumulación de un conjunto. Por ejemplo, la intersección de [0,2] y [-1,1] es [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$

Ejemplo 3

Analicemos ahora el mismo conjunto \( A = [0,1) \) cuando \( X \) está dotado de la topología discreta.

En la topología discreta, todo subconjunto del espacio topológico se considera simultáneamente abierto y cerrado.

  • Conjunto abierto
    En un espacio con topología discreta, cualquier subconjunto de \( X \) es un conjunto abierto. Como \( A \subset X \), se sigue que \( A \) es abierto.
  • Conjunto cerrado
    Del mismo modo, cada subconjunto de \( X \) también es cerrado, ya que su complemento es abierto. Por ejemplo, el complemento \( X/A \), al ser subconjunto de \( X \), también es abierto. Por tanto, \( A \) es cerrado porque su complemento lo es.

Esto implica que todo conjunto en esta topología es clopen, es decir, simultáneamente abierto y cerrado.

En consecuencia, la clausura de un conjunto \( A \) coincide exactamente con \( A \) mismo, ya que no hay necesidad de añadirle ningún punto adicional para que sea cerrado.

$$ \text{Cl}(A) = [0,1) $$

El conjunto cerrado más pequeño que contiene a \( A \) es el propio \( A \).

Nota: Este resultado ilustra cómo la topología del espacio puede alterar profundamente la clausura de un conjunto. Tal como se ha señalado anteriormente, el hecho de que un conjunto sea cerrado no depende de su naturaleza interna, sino de la estructura topológica de \( X \) en la que está inmerso.

Ejemplo 4

Consideremos un espacio topológico \( X \) compuesto por los puntos \( \{a, b, c\} \), provisto de la topología discreta.

En esta topología, todo subconjunto de \( X \) se considera abierto:

  • Los conjuntos \( \emptyset \) y \( \{a, b, c\} \) son abiertos por definición.
  • Los conjuntos unitarios \( \{a\} \), \( \{b\} \), \( \{c\} \) también son abiertos.
  • Cualquier combinación de ellos, como \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \), también se considera abierta.

Además, como el complemento de cualquier subconjunto también pertenece a \( X \) y, por tanto, es abierto, se concluye que en la topología discreta, todos los subconjuntos son simultáneamente abiertos y cerrados.

Si consideramos el conjunto \( A = \{b, c\} \) dentro del espacio \( X \), observamos que es abierto por ser subconjunto de \( X \), y también es cerrado, ya que su complemento \( X/A = \{a\} \) es abierto.

La clausura de \( A \), denotada por \( \text{Cl}(A) \), corresponde a la intersección de todos los conjuntos cerrados que contienen a \( A \). En este caso, no es necesario añadir ningún elemento externo.

Así pues, la clausura de \( A \) es simplemente \( A \) mismo:

\[ \text{Cl}(A) = \{b, c\} \]

En una topología discreta, cada conjunto ya está cerrado, de modo que el proceso de clausura no modifica el conjunto original.

Nota: Como comprobación rápida, los conjuntos cerrados que contienen a \( A \) son \( \{b, c\} \) y \( \{a, b, c\} \). $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ La intersección coincide exactamente con \( A \), por lo tanto, \( \text{Cl}(A) = A \).

El teorema de la clausura de un conjunto

En un espacio topológico \( X \), un elemento \( y \) pertenece a la clausura de un subconjunto \( S \), denotada \( \text{Cl}(S) \), si y solo si todo conjunto abierto \( U \) que contiene a \( y \) intersecta a \( S \) de manera no vacía: \( y \in \text{Cl}(S) \iff \forall \ U \text{ abierto con } y \in U, \ U \cap S \neq \emptyset \).

En términos más intuitivos, para que un punto \( y \in X \) forme parte de la clausura de \( S \), debe estar contenido en todo conjunto abierto que, al mismo tiempo, tenga al menos un punto en común con \( S \).

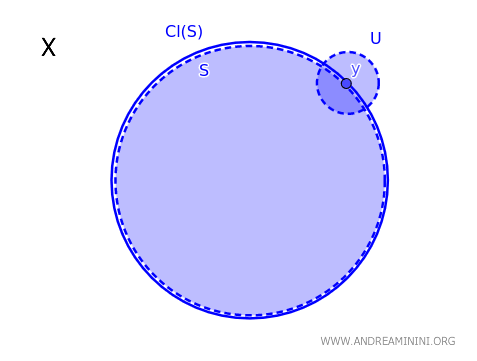
visual example

Este teorema proporciona un criterio fundamental para determinar si un punto pertenece a la clausura de un conjunto \( S \) en un espacio topológico \( X \).

Demostración

  • Condición necesaria: Si \( y \in \text{Cl}(S) \), entonces, por definición, todo entorno abierto que contenga a \( y \) debe intersectar a \( S \). Esto se debe a que la clausura de un conjunto incluye tanto sus puntos interiores como sus puntos adherentes (límite). Un punto límite de \( S \) es aquel en cuya vecindad siempre existe al menos un punto de \( S \), distinto o no del propio \( y \).
  • Condición suficiente: Recíprocamente, si todo conjunto abierto que contiene a \( y \) corta a \( S \), entonces \( y \) debe ser un punto de acumulación de \( S \) o pertenecer directamente a \( S \). En cualquiera de los dos casos, \( y \) queda incluido en \( \text{Cl}(S) \), ya que no existe entorno alguno de \( y \) completamente disjunto de \( S \).

Nota: Este teorema es un pilar de la topología general, ya que conecta de forma precisa la noción de conjunto abierto con la estructura de la clausura. Su utilidad es transversal: interviene en la caracterización de funciones continuas, la convergencia de sucesiones y redes, así como en la demostración de numerosos resultados fundamentales.

Ejemplo

Consideremos el conjunto \( A = (0, 2) \) dentro de la topología estándar sobre \( \mathbb{R} \). Se trata de un intervalo abierto del conjunto de los números reales.

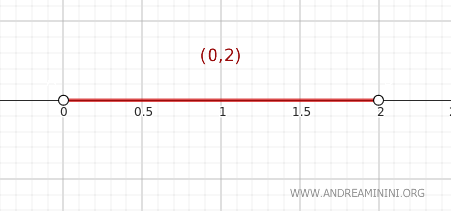
example

Apliquemos el teorema de la clausura para determinar si un punto \( y \) pertenece a \( \text{Cl}(A) \):

Tomemos, por ejemplo, el punto \( y = 2 \in \mathbb{R} \).

De acuerdo con el teorema, \( y \in \text{Cl}(A) \) si y solo si todo conjunto abierto \( U \) que contiene a \( y \) intersecta a \( A \).

  1. Consideración de entornos abiertos de \( y \): Cualquier intervalo abierto que contenga al punto \( y = 2 \), como \( (1.9, 2.1) \), \( (1.95, 2.05) \) o \( (1.99, 2.01) \), contiene necesariamente puntos que pertenecen al intervalo \( A = (0, 2) \). Por ejemplo, los puntos \( 1.95 \) y \( 1.99 \) están claramente dentro de \( A \).
  2. Verificación de la intersección con \( A \): Dado que todo entorno abierto de \( y = 2 \) tiene puntos en común con \( A \), se concluye, conforme al teorema, que \( y = 2 \) pertenece a \( \text{Cl}(A) \).

En efecto, el punto \( y = 2 \) forma parte de la clausura de \( A \), ya que no existe entorno abierto suyo que no interseque a \( A \).

$$ y \in \text{Cl}(A) $$

Así, la clausura del conjunto \( A \) es el intervalo cerrado \( \text{Cl}(A) = [0, 2] \), el cual incluye explícitamente al punto \( y = 2 \).

Propiedades de la clausura en espacios topológicos

En esta sección se examinan diversas propiedades fundamentales de la clausura de un conjunto dentro de un espacio topológico, así como ciertas relaciones sutiles entre operaciones como la clausura y el interior, cuya intuición no siempre resulta inmediata.

Observaciones fundamentales

A continuación se presentan algunas propiedades clave de la clausura, acompañadas de breves justificaciones conceptuales:

Más contenidos próximamente.

 


 
Please feel free to point out any errors or typos, or share suggestions to improve these notes.

FacebookTwitterLinkedinLinkedin

Topología

Ejercicios