Topología Producto de Espacios Topológicos

Dados dos espacios topológicos $X$ y $Y$, la topología producto en $X \times Y$ se define como la topología generada por la base $B$, formada por los productos cartesianos de conjuntos abiertos de la forma $U \times V$, donde $U$ es abierto en $X$ y $V$ es abierto en $Y$. $$ B = \{ U \times V \mid U \text{ es abierto en } X \text{ y } V \text{ es abierto en } Y \} $$

El enfoque inicial para construir una topología sobre $X \times Y$ consiste en considerar conjuntos del tipo $U \times V$, con $U$ abierto en $X$ y $V$ abierto en $Y$.

Esta colección de conjuntos, denotada por $B$, constituye una base para una topología.

Una base topológica es una familia de abiertos tal que cualquier otro conjunto abierto del espacio $X \times Y$ puede expresarse como unión de elementos de dicha familia.

En la topología producto, el producto cartesiano de abiertos sigue siendo un conjunto abierto.

Nota: Los abiertos en la topología producto no se reducen únicamente a productos cartesianos $U \times V$ de abiertos de $X$ y $Y$; también incluyen todas las uniones posibles de tales productos. Por esta razón, la colección $B$ no constituye por sí sola una topología completa, sino únicamente una base. Si consideráramos $B$ como una topología en sí misma, no abarcaría todos los abiertos que pueden obtenerse como uniones de productos cartesianos.

Este principio se extiende también a los conjuntos cerrados.

En la topología producto, el producto cartesiano de conjuntos cerrados es también un conjunto cerrado.

No obstante, no todo conjunto cerrado de la topología producto puede escribirse como un producto de cerrados.

En otras palabras, al igual que ocurre con los conjuntos abiertos, puede haber cerrados en la topología producto que no se derivan de un producto cartesiano de conjuntos cerrados.

Un Ejemplo Práctico
Producto de Múltiples Espacios Topológicos
Base de la Topología Producto
Observaciones Finales

Un Ejemplo Práctico

Veamos un ejemplo concreto que nos ayude a comprender mejor la construcción de la topología producto.

Supongamos que trabajamos con los siguientes espacios topológicos:

$X$ es la recta real $\mathbb{R}$ con su topología usual (los abiertos son los intervalos abiertos $(a, b)$).
$Y$ también es la recta real $\mathbb{R}$ con la misma topología usual.

El producto $X \times Y$ nos da el plano cartesiano $\mathbb{R}^2$.

Para construir la base $B$ de la topología producto sobre $X \times Y$, tomamos todos los productos $U \times V$, con $U$ abierto en $X$ y $V$ abierto en $Y$.

Por ejemplo, consideremos $U = (1, 2) \subset X$, un intervalo abierto en $X$.

Y tomemos $V = (3, 4) \subset Y$, también un intervalo abierto en $Y$.

Entonces, $U \times V = (1, 2) \times (3, 4)$ es un abierto en $\mathbb{R}^2$. Este conjunto representa un rectángulo abierto en el plano cartesiano.

rectángulo abierto en el plano cartesiano

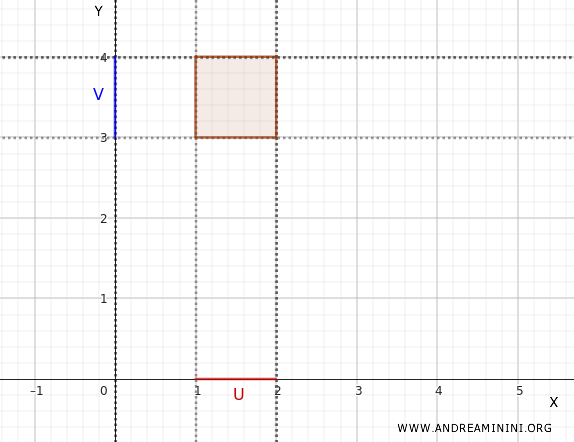
Analicemos ahora qué sucede cuando tomamos la unión de dos conjuntos básicos.

Consideremos $U_1 \times V_1 = (1, 2) \times (3, 4)$.

Y luego $U_2 \times V_2 = (1.5, 2.5) \times (3.5, 4.5)$.

Ambos representan rectángulos abiertos en el plano.

unión de rectángulos abiertos en el plano

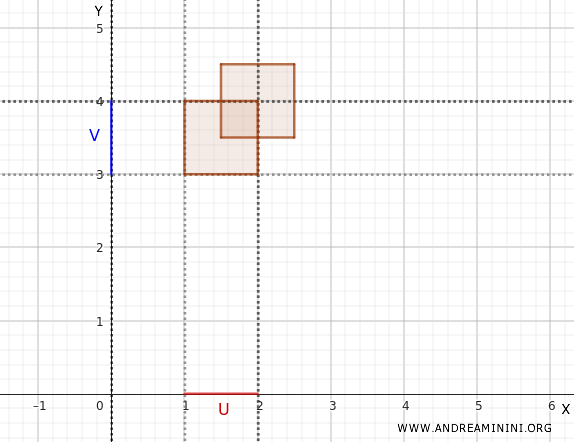
La unión de estos conjuntos ya no tiene la forma de un producto cartesiano $U \times V$, pero al ser unión de elementos de la base, sigue siendo un abierto en la topología producto:

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

Así, cualquier punto del plano puede cubrirse mediante una unión de conjuntos de la base $U \times V$.

Por ejemplo, consideremos el punto $(1.8, 3.8)$.

Este pertenece a $ (1, 2) \times (3, 4) $, por lo que también pertenece a la unión de conjuntos básicos considerada.

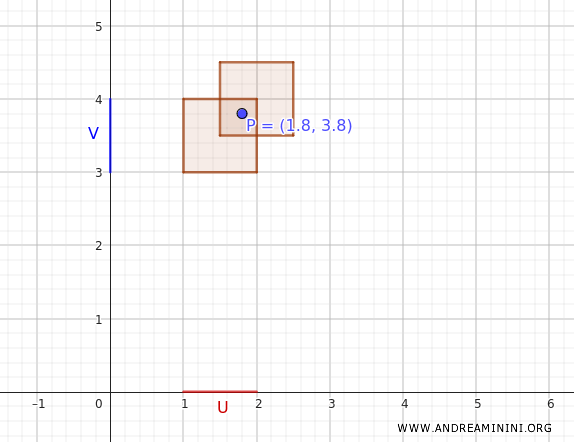
punto contenido en la unión de abiertos básicos

Este ejemplo confirma que la base $B$ genera efectivamente una topología válida sobre el producto cartesiano $X \times Y$.

Nota: Esta topología se denomina "topología producto" y es especialmente valiosa porque conserva la estructura abierta de los espacios originales $X$ y $Y$ al formar el producto $X \times Y$.

Ejemplo 2

Consideremos ahora dos espacios topológicos finitos:

$X = \{a, b, c\}$ con la topología $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$ con la topología $\{\emptyset, \{1\}, Y\}$

Para obtener la topología producto sobre $X \times Y$, calculamos todos los productos cartesianos entre abiertos de $X$ y de $Y$, y luego tomamos todas las uniones posibles entre ellos.

$$ B = \{ U \times V \mid U \text{ es abierto en } X \text{ y } V \text{ es abierto en } Y \} $$

Los abiertos de $X$ son:

$\emptyset$
$\{a\}$
$\{b, c\}$
$X = \{a, b, c\}$

Los abiertos de $Y$ son:

$\emptyset$
$\{1\}$
$Y = \{1, 2\}$

Calculamos ahora los productos cartesianos:

$\emptyset \times \emptyset = \emptyset$
$\emptyset \times \{1\} = \emptyset$
$\emptyset \times Y = \emptyset$
$\{a\} \times \emptyset = \emptyset$
$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \emptyset = \emptyset$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times \emptyset = \emptyset$
$X \times \{1\} = \{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Nota: El producto cartesiano de dos conjuntos se define como el conjunto de pares ordenados donde el primer elemento pertenece al primer conjunto y el segundo al segundo. Formalmente: \[ A \times B = \{(a, b) \mid a \in A \text{ y } b \in B\} \] Si uno de los dos conjuntos es vacío ($\emptyset$), no hay elementos con los que formar pares, y el producto resulta también vacío: \[ \emptyset \times B = \{(a, b) \mid a \in \emptyset \text{ y } b \in B\} = \emptyset \]

La topología producto es el conjunto de todas las uniones posibles de estos productos cartesianos. Por tanto, en $X \times Y$ la topología producto incluye:

$\emptyset$
$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$
Cualquier otra unión de estos conjuntos
Por ejemplo: $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$, etc.

La topología producto en $X \times Y$ está formada, por tanto, por todas estas uniones.

Esto confirma que en la topología producto, los abiertos no son únicamente productos $U \times V$; también lo son las uniones de tales productos.

Por ejemplo: $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$ es un conjunto abierto en la topología producto. Por tanto, no es correcto pensar que los únicos abiertos son los productos $X \times Y$.

La base $B$ de la topología sobre $X \times Y$ está compuesta únicamente por productos cartesianos no vacíos.

$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Producto de Múltiples Espacios Topológicos

El concepto de topología producto se puede extender naturalmente al caso de productos de más de dos espacios topológicos.

Dados $ n $ espacios topológicos $ X_1, X_2, \dots, X_n $, si para cada $ i $ se considera una colección de abiertos $ U_i \subseteq X_i $, entonces el conjunto de todos los productos cartesianos $ U_1 \times U_2 \times \cdots \times U_n $ constituye una base para una topología sobre el espacio producto $ X_1 \times \cdots \times X_n $. $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ es abierto en } X_i \text{ para todo } i \} $$

Base de la Topología Producto

En general, el producto cartesiano de conjuntos abiertos de dos espacios topológicos proporciona una base válida para la topología producto.

$$ B = \{ U \times V \mid U \text{ es abierto en } X \text{ y } V \text{ es abierto en } Y \} $$

Sin embargo, esta base puede ser considerablemente extensa.

Existe un método alternativo, más compacto y eficiente, para construir una base de la topología producto.

Si $ B_X $ es una base de la topología de $ X $ y $ B_Y $ es una base de la topología de $ Y $, entonces el conjunto de productos cartesianos $ U \times V $, con $ U \in B_X $ y $ V \in B_Y $, forma una base para la topología producto sobre $ X \times Y $: $$ B = \{ U \times V \mid U \in B_X \text{ y } V \in B_Y \} $$

Este conjunto $ B $ genera la topología producto sobre $ X \times Y $.

Dicho de otro modo, los elementos de $ B $ son los conjuntos abiertos básicos de la topología producto, y cualquier conjunto abierto en esta topología se puede expresar como unión de estos productos cartesianos.

Nota: Esta construcción se generaliza de forma inmediata al caso de productos finitos. Dados $ n $ espacios topológicos $ X_1, X_2, \dots, X_n $, si $ B_i $ es una base para la topología de $ X_i $, entonces el conjunto de productos $ B_1 \times B_2 \times \cdots \times B_n $ constituye una base para la topología producto en $ X_1 \times \cdots \times X_n $: $$ B = \{ B_1 \times \cdots \times B_n \mid B_i \text{ es base de } X_i, \ i = 1, \dots, n \} $$

Ejemplo

Consideremos dos espacios topológicos finitos:

El espacio $ X = \{a, b\} $ con la topología $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $, cuya base mínima es $ B_X = \{\{a\}, \{b\}\} $.
El espacio $ Y = \{1, 2\} $ con la topología $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $, cuya base mínima es $ B_Y = \{\{1\}, \{2\}\} $.

Podemos construir una base mínima para la topología producto considerando únicamente los productos cartesianos de los elementos de $ B_X $ y $ B_Y $, en lugar de todos los abiertos posibles de $ X $ y $ Y $.

$$ B_X = \{\{a\}, \{b\}\}, \quad B_Y = \{\{1\}, \{2\}\} $$

Sus productos cartesianos son:

$$ \{a\} \times \{1\} = \{(a, 1)\}, \quad \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\}, \quad \{b\} \times \{2\} = \{(b, 2)\} $$

Por tanto, la base mínima de la topología producto en $ X \times Y $ es:

$$ B_{\text{min}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

Esta colección de conjuntos es suficiente para generar toda la topología producto sobre $ X \times Y $.

En resumen, al trabajar con conjuntos atómicos (aquellos que no pueden descomponerse en abiertos más pequeños), obtenemos una base más concisa que sigue describiendo completamente la topología producto.

Demostración

Queremos probar que el conjunto $ B = \{U \times V \mid U \in B_X, V \in B_Y\} $ es una base para la topología producto sobre $ X \times Y $.

Sabemos que $ B_X $ y $ B_Y $ son bases para las topologías respectivas en $ X $ y $ Y $.

Por definición, en la topología producto los abiertos son uniones de conjuntos de la forma $ U \times V $, donde $ U $ y $ V $ son abiertos en $ X $ y $ Y $, respectivamente.

Para demostrar que $ B $ es una base, basta probar que todo abierto $ W \subseteq X \times Y $ puede expresarse como unión de elementos de $ B $.

Verificación de la propiedad de base

Sea $ W $ un abierto en la topología producto, y sea $ (x, y) \in W $.

Entonces, por definición, existe un producto $ U' \times V' \subseteq W $, con $ U' \subseteq X $ y $ V' \subseteq Y $ abiertos, tal que:

$$ (x, y) \in U' \times V' \subseteq W $$

Como $ B_X $ es una base para $ X $, existe $ U \in B_X $ con $ x \in U \subseteq U' $. Análogamente, existe $ V \in B_Y $ tal que $ y \in V \subseteq V' $.

Entonces:

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

Por tanto, para todo punto de $ W $ existe un elemento de $ B $ que lo contiene y está contenido en $ W $.

Conclusión

Como cada punto de un abierto $ W $ está contenido en un conjunto de la base $ B $ que a su vez está contenido en $ W $, se deduce que $ B $ genera la topología producto.

Así, el conjunto $ B = \{U \times V \mid U \in B_X, V \in B_Y\} $ cumple con los requisitos para ser una base de la topología producto sobre $ X \times Y $.

Esto concluye la demostración.

Observaciones Finales

Algunos resultados adicionales relevantes en el contexto de la topología producto:

Teorema del Subespacio Producto
Si $ A \subseteq X $ y $ B \subseteq Y $ son subespacios topológicos, entonces la topología inducida sobre $ A \times B $ como subespacio de $ X \times Y $ coincide con la topología producto construida a partir de las topologías subespacio de $ A $ y $ B $. $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Equivalencia Topológica del Producto
Dados tres espacios $ X, Y, Z $, los espacios topológicos $ (X \times Y) \times Z $, $ X \times (Y \times Z) $ y $ X \times Y \times Z $ son homeomorfos. Es decir, independientemente de cómo se agrupen los factores, el espacio resultante es topológicamente el mismo. $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
Teorema del Interior del Producto Cartesiano
Para dos conjuntos $ A \subseteq X $ y $ B \subseteq Y $, se cumple que el interior de su producto cartesiano es el producto de sus interiores: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$