Teorema del Subespacio para Productos de Espacios
Sean \(A\) y \(B\) dos subconjuntos de espacios topológicos \(X\) y \(Y\), respectivamente, $$ A \subset X $$ $$ B \subset Y $$ la topología en el producto \(A \times B\), considerada como un subespacio de \(X \times Y\), coincide con la topología producto en \(A \times B\) construida a partir de las topologías que \(A\) y \(B\) heredan de \(X\) y \(Y\). $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Aquí, \(\tau_{A \times B}^{\text{sub}}\) denota la topología de subespacio en \(A \times B\) inducida por la topología de \(X \times Y\),
mientras que \(\tau_A^{\text{sub}}\) y \(\tau_B^{\text{sub}}\) son las topologías de subespacio en \(A\) y \(B\) inducidas por \(X\) y \(Y\), respectivamente.
En esencia, este teorema establece que ambos métodos para definir la topología en \(A \times B\) conducen exactamente al mismo resultado.
La topología en \(A \times B\) obtenida como subespacio de \(X \times Y\) es idéntica a la que se obtiene construyendo directamente la topología producto sobre \(A \times B\) a partir de las topologías heredadas de \(A\) y \(B\).
Por tanto, independientemente del procedimiento que sigas, obtendrás la misma estructura topológica en \(A \times B\).
Un Ejemplo Práctico
Veamos ahora un ejemplo para ilustrar el teorema.
Supongamos que tenemos dos espacios topológicos \(X\) y \(Y\). Por ejemplo, considera el plano cartesiano, donde \(X\) corresponde al eje \(x\) y \(Y\) al eje \(y\).
Tomemos ahora dos subconjuntos de estos espacios: \(A\) como subconjunto de \(X\) y \(B\) como subconjunto de \(Y\).
Por ejemplo, \(A\) podría ser un intervalo del eje \(x\), como \([1, 2]\), y \(B\) un intervalo del eje \(y\), como \([3, 4]\).
El producto cartesiano de estos dos subconjuntos, \(A \times B\), está formado por todos los pares \((x, y)\) donde \(x\) pertenece a \(A\) e \(y\) pertenece a \(B\).
En este caso, el producto cartesiano da lugar a un rectángulo en el plano, donde \(x\) varía entre 1 y 2, e \(y\) entre 3 y 4.
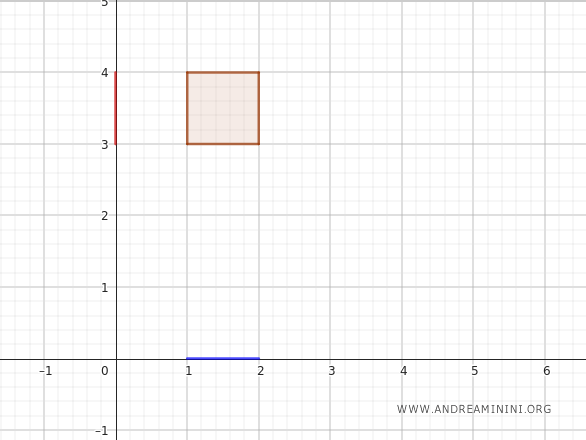
Ahora, consideremos dos maneras de definir una topología sobre \(A \times B\):
- Topología de Subespacio
En este caso, \(A \times B\) se considera como un subespacio de \(X \times Y\), donde \(X \times Y\) representa todo el plano. Así, la topología de \(A \times B\) se obtiene restringiendo la topología de \(X \times Y\) al subconjunto \(A \times B\). - Topología Producto
Alternativamente, podemos construir directamente una topología sobre \(A \times B\) utilizando las topologías que \(A\) y \(B\) heredan de \(X\) y \(Y\). En este enfoque, tratamos a \(A\) y \(B\) como espacios topológicos por derecho propio, y formamos la topología producto sobre \(A \times B\).
Estas dos topologías, la de subespacio y la producto, resultan ser exactamente la misma.
Así que, no importa el enfoque que adoptes, llegarás a la misma estructura topológica en \(A \times B\).
Y así sucesivamente...