Puntos fijos en topología
En topología, un punto fijo es aquel valor que se mantiene constante bajo la aplicación de una función.
De manera simple, si contamos con una función f(x), se dice que p es un punto fijo si se cumple que f(p) = p. Esto significa que la salida de la función es igual a su entrada cuando se evalúa en p.
$$ f(p) = p $$
Imagina que giras un objeto alrededor de un punto central P.
Este giro asigna nuevas coordenadas a los puntos del objeto en el espacio, pero sin cambiar el punto P.
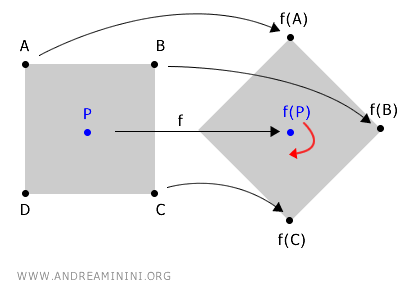
En este caso, el centro de rotación, P, funciona como un punto fijo porque sus coordenadas no varían con la función de rotación f(P).
$$ f(P) \longrightarrow P $$
Los puntos fijos son fundamentales en distintas áreas y aplicaciones de la matemática, como en análisis numérico, teoría de juegos y economía.
Un ejemplo destacado en topología es el Teorema del Punto Fijo de Brouwer.
Un ejemplo práctico
Consideremos la función f(x) = sin(x) en el intervalo cerrado [0, 2π] radianes.
$$ f(x) = \sin(x) $$
En p=0 radianes, el punto fijo de la función es claro, ya que sin(0) = 0.
$$ \sin(0) = 0 $$
Aquí, la salida es exactamente igual a la entrada.
Ejemplo 2
Ahora considera la función f(x) = cos(x) en el mismo intervalo [0, 2π] radianes.
$$ f(x) = \cos(x) $$
En este caso, x=0 no es un punto fijo pues cos(0) = 1, lo que muestra una diferencia entre la entrada y la salida.
El punto fijo para la función f(x) = cos(x) se encuentra aproximadamente en x = 0.73908513
$$ \cos(0.73908513) = 0.73908513 $$
De este modo, cos(0.73908513) es casi exactamente 0.73908513.
El Teorema del Punto Fijo de Brouwer
Este teorema establece:
Cualquier función continua que mapea un intervalo cerrado de n dimensiones asegura al menos un punto fijo.
Es un teorema de existencia, que subraya la garantía de al menos un punto fijo, sin especificar su ubicación precisa.
Este principio tiene implicaciones importantes, especialmente en la demostración de la existencia de estados de equilibrio en sistemas dinámicos y modelos económicos.
Y así sucesivamente.