Topología Digital
La topología digital estudia las estructuras topológicas definidas sobre espacios discretos, como una malla de puntos (píxeles en 2D o vóxeles en 3D), describiendo las propiedades de conexión entre ellos según una relación de adyacencia determinada.
En este marco, los conjuntos abiertos se caracterizan por las conexiones entre puntos, donde el tipo de conexión depende de criterios como la conectividad 4, la conectividad 8 (en 2D) o la conectividad 6, 18 y 26 (en 3D).
La topología digital tiene amplias aplicaciones en campos como el procesamiento de imágenes, los gráficos digitales y la visión por computador, ya que adapta conceptos de la topología clásica a entornos discretos.
Conjuntos Abiertos en Topología Digital
En topología digital, un conjunto \(U\) se considera abierto si, para cada punto \(x \in U\), todos sus puntos adyacentes - según la conectividad establecida - también pertenecen a \(U\).
La noción de “adyacencia” o “vecindad” entre puntos depende del tipo de conectividad elegido en el espacio digital. Por ejemplo:
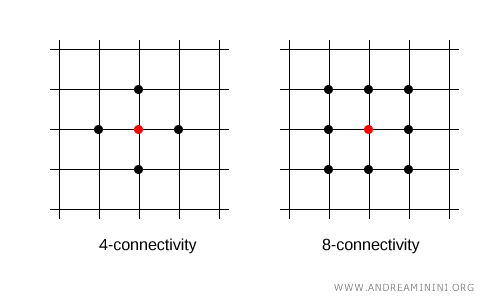
En una cuadrícula anular o circular, cada punto es adyacente a otros dos, configurando una estructura de conectividad 2.
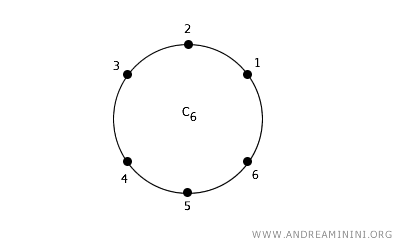
En el plano 2D, un punto puede estar conectado a cuatro vecinos (conectividad 4) - norte, sur, este y oeste - o a ocho vecinos (conectividad 8), incluyendo los puntos en diagonal.
En un espacio digital tridimensional (3D), la conexión entre puntos puede regirse por criterios de conectividad 6, 18 o 26, dependiendo del número de vecinos considerados.
Ejemplo
Supongamos un conjunto de puntos dispuestos en un círculo digital (espacio discreto) con conectividad 2.
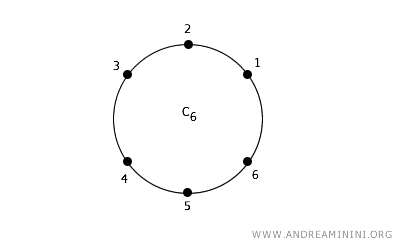
En esta configuración, cada punto tiene dos vecinos inmediatos, uno a su izquierda y otro a su derecha.
Por ejemplo, el punto 2 es adyacente a los puntos 1 y 3.

En este caso, un conjunto \(U\) es abierto en topología digital si todos los vecinos de cada punto en \(U\) también pertenecen al conjunto.
Este concepto traduce, en espacios discretos, la idea de continuidad y de conexión entre puntos.
Diferencia entre Topología Digital y Topología Discreta
Aunque tanto la topología digital como la topología discreta se desarrollan sobre espacios discretos, presentan diferencias fundamentales:
- Topología Discreta
Una topología sobre un conjunto \(X\) se denomina discreta cuando todo subconjunto de \(X\) es abierto. - Topología Digital
En cambio, en topología digital, un subconjunto es abierto únicamente si respeta las condiciones de conectividad impuestas entre los puntos.
¿Cuál es, entonces, la diferencia clave?
En la topología discreta, cualquier subconjunto es abierto. En la topología digital, solo se consideran abiertos aquellos conjuntos que cumplen los criterios de conectividad establecidos.
Por tanto, la topología digital no es equivalente a la topología discreta, ya que no todos los subconjuntos son necesariamente abiertos.
Por ejemplo, un conjunto compuesto por dos píxeles aislados - sin conexión entre ellos - no sería abierto en topología digital, mientras que sí lo sería en topología discreta.
En resumen, la topología digital está diseñada para reflejar la conectividad entre puntos en un espacio digital, mientras que la topología discreta considera cada punto como una entidad independiente, sin relaciones de adyacencia.
Ejemplo
Consideremos el conjunto de puntos \(\{1, 2, 3, 4\}\) dispuestos en una estructura circular, con una topología digital basada en conectividad 2.
- El conjunto \(\{1, 2\}\) es abierto en topología digital, ya que los puntos 1 y 2 son adyacentes.
- El conjunto \(\{1, 3\}\) no es abierto, dado que los puntos 1 y 3 no están conectados directamente.
Si analizáramos estos mismos puntos \(\{1, 2, 3, 4\}\) bajo la topología discreta, tanto \(\{1, 2\}\) como \(\{1, 3\}\) serían conjuntos abiertos, ya que en este caso cualquier subconjunto lo es.
Nota. En el mismo espacio métrico discreto \(\{1, 2, 3, 4\}\), la topología digital resulta ser más restrictiva que la topología discreta, al exigir una condición de conectividad para la apertura de conjuntos.
Y así sucesivamente.