La Topología Estándar de un Conjunto Abierto

La topología estándar en $ \mathbb{R} $ se define a partir de los intervalos abiertos $ (a, b) $, con $ a < b $, y de cualquier unión, finita o infinita, de estos intervalos, que se consideran conjuntos abiertos.

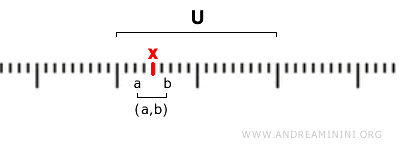
En términos precisos, un conjunto $ U $ es abierto si, para cada punto $ x \in U $, existe un intervalo abierto $ (a, b) $ tal que $ x \in (a, b) $ y, además, $ (a, b) \subseteq U $.

$$ x \in (a,b) \subseteq U $$

En otras palabras, cada elemento $ x $ de un conjunto abierto $ U $ está contenido en un intervalo abierto que, a su vez, está completamente incluido en $ U $.

ejemplo de un conjunto abierto

En la topología estándar, se consideran abiertos los siguientes tipos de conjuntos:

Intervalos abiertos
Los conjuntos abiertos en la topología estándar de $ \mathbb{R} $ son precisamente los intervalos abiertos $ (a, b) $ con $ a < b $, junto con cualquier unión arbitraria de estos intervalos, sin importar si la colección es finita o infinita.
Operaciones con conjuntos abiertos
En esta topología, las operaciones de unión e intersección finita preservan la apertura.
- Uniones: La unión de cualquier familia de conjuntos abiertos es siempre un conjunto abierto.
- Intersecciones finitas: La intersección de un número finito de conjuntos abiertos también es un conjunto abierto.

La topología estándar es solo una de las muchas topologías que pueden definirse sobre un conjunto $ X $. Se le denomina "estándar" porque es la más utilizada y desempeña un papel fundamental en diversas ramas de las matemáticas.

Se adopta esta topología porque modela de manera natural nociones intuitivas de proximidad, apertura y continuidad, especialmente en la recta real $ \mathbb{R} $.

Nota: En $ \mathbb{R} $ y en otros espacios, existen topologías alternativas con bases distintas, lo que da lugar a conjuntos abiertos que obedecen reglas diferentes. Estas variaciones suelen diseñarse para estudiar propiedades específicas o para analizar estructuras matemáticas desde perspectivas alternativas.

Ejemplo Práctico

La base de la topología estándar en $ \mathbb{R} $ está formada por todos los intervalos abiertos $ (a, b) $, con $ a < b $.

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

Un aspecto clave de esta topología es que, para cualquier punto $ x $ dentro de un conjunto abierto $ U $, siempre es posible encontrar un intervalo abierto centrado en $ x $ que esté completamente contenido en $ U $, lo que satisface la definición de conjunto abierto en la topología estándar.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

Donde $ U $ es un conjunto abierto en la topología estándar de $ \mathbb{R} $.

Se le denomina "estándar" porque es la topología más utilizada en la recta real y porque permite formalizar de manera natural los conceptos de continuidad y límite.

Ejemplo 2

Consideremos el intervalo real $ (0,1) $, excluyendo los extremos $ 0 $ y $ 1 $, y analicemos su estructura topológica bajo la topología estándar.

Nos interesa determinar si este conjunto puede considerarse un espacio topológico.

el caso del intervalo (0,1)

En términos de la topología inducida, un subconjunto $ U \subset (0, 1) $ es abierto en $ (0,1) $ si, para cada punto $ x \in U $, existe un intervalo abierto $ (a, b) $ en $ \mathbb{R} $ tal que $ x \in (a, b) $ y además se cumple que $ (a, b) \cap (0,1) \subseteq U $.

Observemos que el intervalo $ (0,1) $ puede escribirse como la intersección de conjuntos abiertos en la topología estándar de $ \mathbb{R} $, lo que confirma que hereda una estructura topológica bien definida.

Por lo tanto, el intervalo $ (0,1) $ es un espacio topológico con la topología inducida por la topología estándar de $ \mathbb{R} $.

Por ejemplo, los intervalos $ (0.1, 0.5) $, $ (0.2, 0.9) $ o sus uniones, como $ (0.1, 0.5) \cup (0.6, 0.8) $, son conjuntos abiertos en $ (0,1) $ bajo la topología inducida. En otras palabras, los conjuntos abiertos en $ (0,1) $ son precisamente aquellos conjuntos abiertos en $ \mathbb{R} $ que, al intersectarse con $ (0,1) $, permanecen en su totalidad dentro del intervalo.

Como $ (0,1) $ es un subespacio de $ \mathbb{R} $ bajo la topología inducida, cumple todas las propiedades fundamentales de un espacio topológico.

Ejemplo 3

Consideremos el conjunto finito $ X = \{1,2,3\} $, compuesto por tres números enteros.

Queremos determinar si $ X $ puede dotarse de una estructura topológica bajo la topología estándar de $ \mathbb{R} $.

En este caso, los elementos individuales de $ X $ no pueden considerarse abiertos, ya que la base de la topología estándar de $ \mathbb{R} $ está formada por intervalos abiertos, lo que no se adapta naturalmente a un conjunto discreto como $ X $.

Por ejemplo, si consideramos el elemento $ \{2\} $ dentro del conjunto $ X $, este está contenido en un intervalo abierto $ (2-\epsilon, 2+\epsilon) $, pero dicho intervalo incluye infinitos números reales que no pertenecen a $ X $. Por lo tanto, el conjunto $ \{2\} $ no satisface la definición de conjunto abierto en la topología estándar de $ \mathbb{R} $.
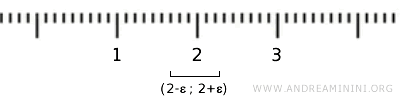
ejemplo con el número 2

Si consideramos $ X $ como un subconjunto de $ \mathbb{R} $, la "topología inducida" o "topología de subespacio" en $ X $ solo permite dos conjuntos abiertos: el conjunto vacío y el propio conjunto $ X $, lo que resulta trivial desde el punto de vista topológico.

Para dotar a un conjunto finito como $ X $ de una estructura topológica más rica, suele emplearse la topología discreta, en la que todos los subconjuntos de $ X $ son abiertos por definición.

Y así sucesivamente.