Espacio Topológico Normal

Un espacio topológico $ X $ se dice normal si cumple con las siguientes dos condiciones:

Los conjuntos unitarios son cerrados
Es decir, para todo punto $ x \in X $, el conjunto $\{x\}$ debe ser cerrado en la topología dada.
Cualquier par de conjuntos cerrados y disjuntos puede separarse mediante conjuntos abiertos disjuntos
Si $ A $ y $ B $ son conjuntos cerrados que no tienen puntos en común (es decir, $ A \cap B = \emptyset $), entonces existen dos conjuntos abiertos $ U $ y $ V $ tales que:
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $ (no se intersectan).

La noción de normalidad radica en que, en estos espacios, siempre es posible "encerrar" dos conjuntos cerrados disjuntos dentro de conjuntos abiertos separados que no se superponen.

En otras palabras, la normalidad garantiza que, siempre que dos conjuntos cerrados sean disjuntos, podemos hallar entornos abiertos disjuntos que los contengan.

Esta propiedad es clave en la construcción de funciones continuas capaces de distinguir puntos dentro del espacio.

Ejemplo Práctico
Notas Adicionales

Ejemplo Práctico

Consideremos el espacio topológico $ X = \mathbb{R} $ con la topología estándar, generada por los intervalos abiertos de la forma $ (a, b) $.

Tomemos como ejemplo dos conjuntos cerrados y disjuntos en $ \mathbb{R} $:

$ A = \{0\} $, un conjunto reducido a un solo punto.
$ B = [2, 3] $, un intervalo cerrado.

Ambos conjuntos son cerrados en la topología estándar de $ \mathbb{R} $ y, al no compartir elementos, son disjuntos.

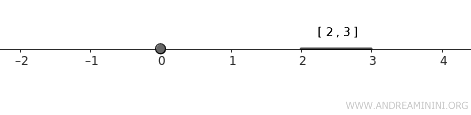
example

Nota. El conjunto $ A $ contiene un único punto y no incluye ningún entorno a su alrededor, lo que lo hace cerrado. Por otro lado, $ B $ es un intervalo cerrado, por lo que también es un conjunto cerrado.

Ahora, buscamos dos conjuntos abiertos disjuntos que los contengan.

Una posible elección es $ U = (-1, 1) $, un entorno abierto que contiene a $ A = \{0\} $.

$$ A \subset U = (-1,1) $$

Para $ B = [2,3] $, podemos tomar $ V = (1, 4) $, un entorno abierto que lo contiene completamente.

$$ B \subset V = (1,4) $$

Los conjuntos abiertos $ U $ y $ V $ son disjuntos, ya que no se superponen ($ U \cap V = \emptyset $).

Esto confirma que $ \mathbb{R} $, con su topología estándar, es un espacio normal.

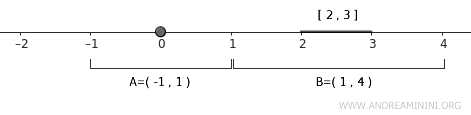
example

Este mismo razonamiento se aplica a cualquier otro par de conjuntos cerrados disjuntos: siempre es posible encontrar conjuntos abiertos disjuntos que los contengan.

Por lo tanto, la recta real $ X = \mathbb{R} $, equipada con la topología estándar, es un espacio normal.

Notas Adicionales

Algunos puntos clave sobre los espacios normales:

La recta real $ \mathbb{R} $ con la topología estándar es un espacio normal
No solo satisface la condición de regularidad (lo que significa que podemos separar un punto de un conjunto cerrado mediante conjuntos abiertos disjuntos), sino que también cumple con el criterio más fuerte de normalidad.
Todo espacio métrico es normal
Si un espacio posee una métrica que define distancias entre sus puntos, entonces siempre es normal.
Todo espacio normal es también regular
Es decir, la normalidad es una propiedad más fuerte que la regularidad.

Y así sucesivamente.