Bola Abierta

En topología, una bola abierta - también llamada vecindad circular, disco o esfera abierta - es el conjunto de todos los puntos que se encuentran a una distancia menor que un cierto valor de un punto fijo, denominado centro $ c $. Dicha distancia se conoce como radio $ r $: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Este concepto se define en el contexto de un espacio métrico ($ M $), donde $ d $ es una métrica, es decir, una función que mide la distancia entre puntos en dicho espacio.

Una bola abierta queda completamente determinada por su centro y su radio.

Se dice que es "abierta" en el sentido topológico porque cualquier punto dentro de la bola pertenece, a su vez, a una bola más pequeña que está completamente contenida en la original.

Nota: Las bolas abiertas son invariantes bajo escalamiento y traslación. Es decir, cambiar su tamaño o moverlas en el espacio no altera su naturaleza.

Consideremos el caso del plano $ \mathbb{R}^2 $. En este contexto, la distancia entre un punto $ p = (x, y) $ y otro punto $ c = (x_0, y_0) $, que actúa como centro, se mide mediante la métrica euclidiana:

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

Las bolas abiertas desempeñan un papel fundamental en la construcción de la estructura topológica de los espacios métricos. En particular, sirven como base para definir la topología estándar del plano $ \mathbb{R}^2 $.

Esta topología se construye a partir del siguiente conjunto de bolas abiertas:

$$ B = \{ B(p, r) \ | \ p \in \mathbb{R}^2, \ r > 0 \} $$

Aquí, $ p $ representa un punto $ (x,y) $ en el plano, y $ r $ es el radio de la bola.

la topología estándar en R^2

Si bien existen muchas otras topologías posibles sobre $ \mathbb{R}^2 $, la topología inducida por las bolas abiertas euclidianas es, con diferencia, la más habitual.

Dentro de una bola abierta, cualquier punto $ q \in B(p,r) $ es, a su vez, el centro de otra bola abierta más pequeña $ B(q, \epsilon) $, que queda completamente contenida en $ B(p,r) $.

Esto se expresa formalmente como:

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ \text{tal que} \ B(q,\epsilon) \subset B(p,r) $$

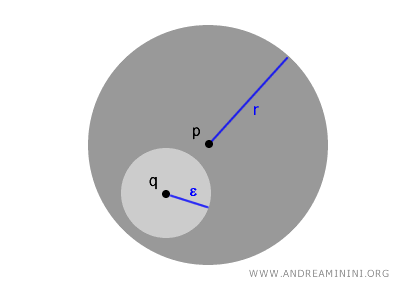
ejemplo de una bola abierta

Este proceso puede repetirse de manera indefinida, reflejando la naturaleza de las bolas abiertas dentro de la estructura de un espacio topológico.