Teorema sobre el Interior del Producto Cartesiano
Dados dos conjuntos \(A\) y \(B\) contenidos respectivamente en dos espacios topológicos \(X\) y \(Y\), el interior de su producto cartesiano \(A \times B\) coincide con el producto de sus interiores. Es decir: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
Esta propiedad se verifica en particular para conjuntos abiertos en el contexto del producto de dos espacios topológicos.
En términos más sencillos, el teorema afirma que, dados conjuntos \(A\) y \(B\) en espacios topológicos \(X\) y \(Y\), el interior de su producto cartesiano puede determinarse tomando el producto de los interiores de \(A\) y \(B\).
Un Ejemplo Práctico
Consideremos los espacios topológicos \(X = \mathbb{R}\) y \(Y = \mathbb{R}\), junto con los subconjuntos \(A = (0, 2)\) y \(B = (1, 3)\).
Observemos que \(A\) y \(B\) son intervalos abiertos en la recta real \(\mathbb{R}\).
Comencemos por determinar los interiores de ambos conjuntos.
El interior de \(A\) es precisamente (0,2), ya que \(A\) es un intervalo abierto, por lo que su interior coincide con el propio conjunto.
$$ \text{Int}(A) = (0, 2) $$
De manera análoga, el interior de \(B\) es (1,3).
$$ \text{Int}(B) = (1, 3) $$
Ahora calculemos el producto cartesiano de los interiores \(\text{Int}(A) \times \text{Int}(B)\):
$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$
Este producto cartesiano corresponde al conjunto de todos los pares \((x, y)\) tales que \(x \in (0, 2)\) y \(y \in (1, 3)\).
$$ \text{Int}(A) \times \text{Int}(B) = \{(x, y) \mid x \in (0, 2) \text{ y } y \in (1, 3)\} $$
Este conjunto puede visualizarse como un rectángulo abierto en el plano \(\mathbb{R}^2\), delimitado por los vértices \((0, 1)\), \((0, 3)\), \((2, 1)\) y \((2, 3)\).
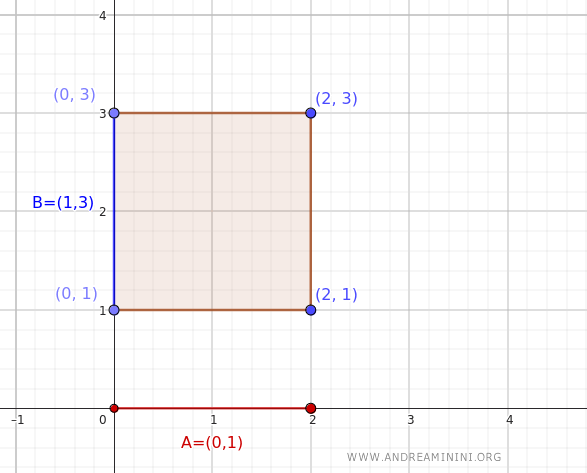
Procedamos ahora a calcular el interior del producto cartesiano \(A \times B = (0, 2) \times (1, 3)\):
Obtenemos exactamente el mismo conjunto: el rectángulo abierto en \(\mathbb{R}^2\).
De este modo, el interior del producto cartesiano \(\text{Int}(A \times B)\) coincide con el producto de los interiores \(\text{Int}(A) \times \text{Int}(B)\).
$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$
Este ejemplo ilustra claramente la validez del teorema.
Demostración
La demostración se estructura en dos etapas. Primero, probaremos que el interior del producto cartesiano contiene el producto de los interiores, y luego que está contenido en él, concluyendo así que ambos conjuntos son iguales.
1] El Interior del Producto Cartesiano Contiene el Producto de los Interiores
En esta primera parte, queremos demostrar que
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
Es decir, debemos probar que todo par \((x, y)\) tal que \(x \in \text{Int}(A)\) y \(y \in \text{Int}(B)\) pertenece al interior de \(A \times B\).
Como \(x\) es un punto interior de \(A\), existe un abierto \(U\) de \(X\) tal que \(x \in U \subseteq A\).
De manera análoga, como \(y\) es un punto interior de \(B\), existe un abierto \(V\) de \(Y\) tal que \(y \in V \subseteq B\).
El producto \(U \times V\) es un conjunto abierto en el producto topológico \(X \times Y\) que contiene al par \((x, y)\).
Además, \(U \times V\) está contenido en \(A \times B\), lo que demuestra que \((x, y)\) pertenece a \(\text{Int}(A \times B)\).
Así, hemos verificado que \(\text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B)\).
2] El Producto de los Interiores Contiene el Interior del Producto Cartesiano
Ahora, demostraremos que
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
Esto equivale a probar que si \((x, y) \in \text{Int}(A \times B)\), entonces \(x \in \text{Int}(A)\) y \(y \in \text{Int}(B)\).
Tomemos un par \((x, y)\) perteneciente a \(\text{Int}(A \times B)\).
Por definición, existe un abierto \(W\) de \(X \times Y\) tal que \((x, y) \in W \subseteq A \times B\).
En el contexto de la topología producto, podemos encontrar abiertos \(U\) en \(X\) y \(V\) en \(Y\) tales que \((x, y) \in U \times V \subseteq W\).
De la inclusión \(U \times V \subseteq A \times B\) se deduce que \(U \subseteq A\) y \(V \subseteq B\).
Por tanto, \(x\) pertenece al interior de \(A\) y \(y\) pertenece al interior de \(B\).
Concluimos así que \((x, y) \in \text{Int}(A) \times \text{Int}(B)\), lo que prueba que \(\text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B)\).
3] Conclusión
Hemos demostrado ambas inclusiones:
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
Por tanto, concluimos que el interior del producto cartesiano \(A \times B\) coincide con el producto de los interiores de \(A\) y \(B\).
$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
Así queda establecido el teorema.