Teorema de la Base en la Topología de Subespacios
Dado un espacio topológico \(X\) con una base \( B_X \)—una colección de conjuntos abiertos que "genera" la topología en \(X\)—y un subconjunto \(Y\) de \(X\), la colección de intersecciones de los elementos de \( B_X \) con \(Y\) forma una base \( B_Y \) para la topología de subespacio en \(Y\). $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$
Ejemplo
Vamos a clarificar este concepto con un ejemplo sencillo.
Consideremos el espacio topológico \( \mathbb{R} \) con la topología estándar, cuya base es el conjunto de intervalos abiertos \((a, b)\), donde \( a < b \).
Ahora, tomemos el subconjunto \(Y = [0, 2]\) de \( \mathbb{R} \).
Queremos encontrar una base para la topología de subespacio en \(Y\).
La base para la topología estándar en el conjunto de los números reales \( \mathbb{R} \) es:
$$ B_{\mathbb{R}} = \{(a, b) \ | \ a, b \in \mathbb{R}, \ a < b \} $$
Nota: La base para los números reales es una colección de conjuntos (a,b) con \(a < b\) donde \(a\) y \(b\) son números reales. Cualquier conjunto abierto en \( \mathbb{R} \) puede expresarse como una unión de tales intervalos abiertos. Por ejemplo, el conjunto abierto (0,3) se puede obtener uniendo los conjuntos abiertos (0,2) ∪ (1,3). De manera similar, el conjunto abierto (2,5) se puede obtener uniendo los conjuntos abiertos (2,4) ∪ (3,6).
La base para la topología de subespacio en \(Y\) es la intersección de todos los conjuntos abiertos (a,b) en la base de \( \mathbb{R} \) con el conjunto \(Y = [0,2]\).
$$ B_Y = \{ (a, b) \cap [0, 2] \ | \ (a, b) \in B_{\mathbb{R}} \} $$
Algunos elementos que pueden formar parte de \( B_Y \) son:
Por ejemplo, tomemos el conjunto abierto \( (a, b) = (-1, 1) \) en la topología de \( \mathbb{R} \).
$$ (-1, 1) \cap [0, 2] = [0, 1) $$
Entonces, \([0, 1) \) es un elemento que pertenece a la base \( B_Y \).
A continuación, tomemos \( (a, b) = (1, 3) \) en la topología de \( \mathbb{R} \).
$$ (1, 3) \cap [0, 2] = (1, 2] $$
Por lo tanto, \( (1, 2] \) es otro elemento de la base \( B_Y \).
Ahora, tomemos \( (a, b) = (0.5, 1.5) \) en la topología de \( \mathbb{R} \).
$$ (0.5, 1.5) \cap [0, 2] = (0.5, 1.5) $$
Así, \( (0.5, 1.5) \) también es un elemento de \( B_Y \). Y así sucesivamente.
Verifiquemos la base \( B_Y \):
Consideremos un conjunto abierto \(W\) en la topología de subespacio en \(Y\), por ejemplo \(W = (0.5, 1.5]\).
El conjunto \(W = (0.5, 1.5] \) es abierto en \(Y\) porque existe un conjunto abierto \(U\) en \( \mathbb{R} \) tal que \(W = U \cap [0, 2]\). Por ejemplo, \(U = (0.5, 1.5]\).
$$ W = U \cap [0, 2] = (0.5, 1.5] \cap [0, 2] = (0.5,1.5] $$
Consideremos un punto \(y \in W\), por ejemplo \( y = 1 \).
Como \(U = (0.5, 1.5]\) es abierto en \( \mathbb{R} \), existe un elemento de la base \( (a, b) \in B_{\mathbb{R}} \) tal que \( y \in (a, b) \subseteq U \).
En este caso, podemos tomar \( (a, b) = (0.8, 1.2) \).
Al intersectar \( (a, b) \) con \( [0, 2] \) obtenemos:
$$ (0.8, 1.2) \cap [0, 2] = (0.8, 1.2) $$
Entonces, \( (0.8, 1.2) \) es un elemento de \( B_Y \) que contiene \( y = 1 \) y está en \( W = (0.5, 1.5] \).
Esto confirma que cada punto de \( W \) está cubierto por un elemento de \( B_Y \), demostrando que \( B_Y \) es una base para la topología de subespacio en \(Y\).
Demostración
En topología, consideremos un subconjunto \(X \subset Y\).
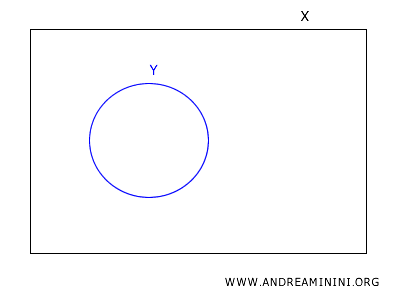
La base \(B_Y\) es la colección de conjuntos formados al intersectar cada elemento de la base \(B_X\) con el subconjunto \(Y\).
Cada elemento de \(B_Y\) es un conjunto abierto en la topología de subespacio en \(Y\).
Necesitamos demostrar que \(B_Y\) es una base para la topología de subespacio en \(Y\).
Consideremos un conjunto abierto \(W\) en la topología de subespacio en \(Y\).
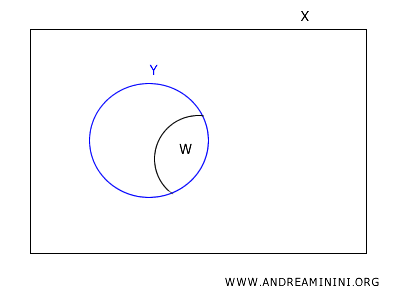
Dado que \(W\) es abierto en \(Y\), existe un conjunto abierto \(U\) en \(X\) tal que \(W = U \cap Y\).
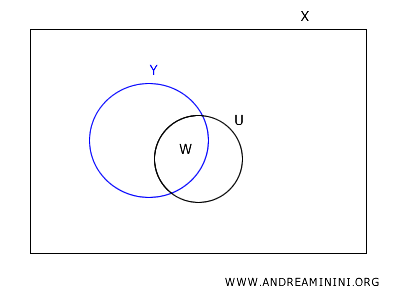
Tomemos cualquier punto \(y\) en \(W\).
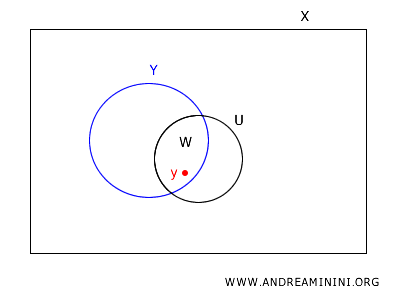
Como \(U\) es abierto en \(X\), por la definición de una base, existe un elemento de la base \(B \in B_X\) tal que \(y \in B \subseteq U\).
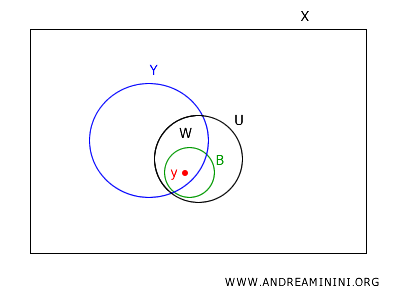
Al intersectar \(B\) con \(Y\), obtenemos \(B \cap Y \in B_Y\), que contiene a \(y\) y está dentro de \(W\). Por lo tanto, cada punto en \(W\) está cubierto por un elemento de \(B_Y\).
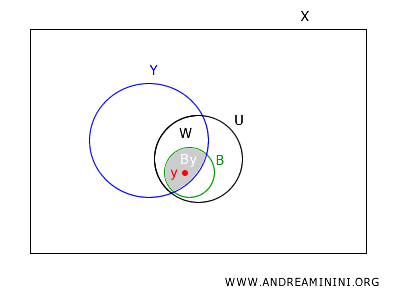
En conclusión, cada punto \(y\) en \(W\) está contenido en un elemento de \(B_Y\) que también está contenido en \(W\).
$$ y \in B_Y = B \cap Y \subseteq U \cap Y = W $$
Esto demuestra que \(B_Y\) es una base para la topología de subespacio en \(Y\).
Y así sucesivamente.