La Unión de los Interiores de Dos Conjuntos
La unión de los interiores de dos conjuntos $ A $ y $ B $ siempre está contenida en el interior de su unión: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] No obstante, esta inclusión no siempre es una igualdad.
Este resultado nos dice que el interior de la unión de dos conjuntos es, como mínimo, tan grande como la unión de sus interiores.
Sin embargo, en general, estas dos expresiones no coinciden. Es decir, no siempre se cumple que:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Es perfectamente posible que la inclusión sea estricta.
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Esta diferencia es clave para entender cómo se relacionan los conjuntos y sus interiores en el contexto de la topología.
Un Ejemplo Ilustrativo
Consideremos dos intervalos abiertos \( A \) y \( B \) en \(\mathbb{R}\) con la topología usual:
$$ A = (0, 2) $$
$$ B = (1, 3) $$
Dado que el interior de un intervalo abierto coincide con el propio intervalo, tenemos:
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
Por lo tanto, la unión de los interiores es:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
Al calcular la unión de estos intervalos, obtenemos:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
Por otro lado, la unión de los conjuntos \( A \) y \( B \) es:
$$ A \cup B = (0, 2) \cup (1, 3) $$
Dado que los intervalos se solapan, su unión se simplifica a:
$$ A \cup B = (0, 3) $$
El interior de la unión \( A \cup B \) es:
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
Verificamos ahora la propiedad:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
En este caso particular, se cumple que la unión de los interiores coincide con el interior de la unión:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
No obstante, esto no siempre ocurre.
Por ejemplo, si en lugar de intervalos abiertos tomamos intervalos cerrados: $$ A = [0, 2] $$ $$ B = [2, 3] $$ Los interiores de estos conjuntos son: $$ \text{Int}(A) = (0, 2) $$ $$ \text{Int}(B) = (2, 3) $$ Mientras que el interior de la unión $ A \cup B = [0, 3] $ es el intervalo $ (0, 3) $: $$ \text{Int}(A \cup B) = (0,3) $$ En este caso, la inclusión sigue siendo válida porque $ (0, 2) \cup (2, 3) $ está contenido en $ (0, 3) $: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ Sin embargo, la igualdad no se cumple, ya que el punto $ 2 $ pertenece al interior de la unión: $$ 2 \in \text{Int}(A \cup B) = (0, 3) $$ pero no pertenece al interior de ninguno de los dos conjuntos originales: $$ 2 \not \in \text{Int}(A) $$ $$ 2 \not \in \text{Int}(B) $$ En consecuencia, $ 2 $ no está en la unión de los interiores: $$ 2 \not \in \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) $$ Esto demuestra que los conjuntos no son iguales: $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ Así, en general, la unión de los interiores de dos conjuntos siempre está contenida en el interior de su unión, pero la igualdad no siempre se cumple.
Ejemplo 2
Ahora consideremos dos intervalos abiertos que no se solapan, por ejemplo:
$$ A = (0, 1) $$
$$ B = (2, 3) $$
El interior de cada intervalo es el propio intervalo, ya que ambos son abiertos:
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
Por lo tanto, la unión de los interiores es:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
La unión de los intervalos \( A \) y \( B \) es:
$$ A \cup B = (0, 1) \cup (2, 3) $$
El interior de la unión \( A \cup B \) es:
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
Verificamos la propiedad:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
En este caso, también se cumple que:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Con estos ejemplos en \(\mathbb{R}\), hemos demostrado que la unión de los interiores de dos intervalos está siempre contenida en el interior de su unión. Además, en estos casos específicos, la igualdad también se cumple:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Sin embargo, como ya mencionamos, en espacios más complejos, una superposición parcial puede dar lugar a inclusión sin igualdad.
Ejemplo 3
Ahora consideremos dos conjuntos \( A \) y \( B \) en el plano real \(\mathbb{R}^2\) con la topología usual.
Los conjuntos \( A \) y \( B \) son dos discos abiertos que se solapan parcialmente, centrados en \( (0, 0) \) y \( (0.5, 0) \), respectivamente, ambos con radio \( 1 \):
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$
En el caso de conjuntos abiertos como \( A \) y \( B \), su interior coincide con el propio conjunto:
$$ \text{Int}(A) = A $$
$$ \text{Int}(B) = B $$
Por lo tanto, la unión de los interiores es simplemente la unión de los dos discos:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
La unión de los conjuntos \( A \) y \( B \) es la región formada por ambos discos que se intersectan parcialmente.
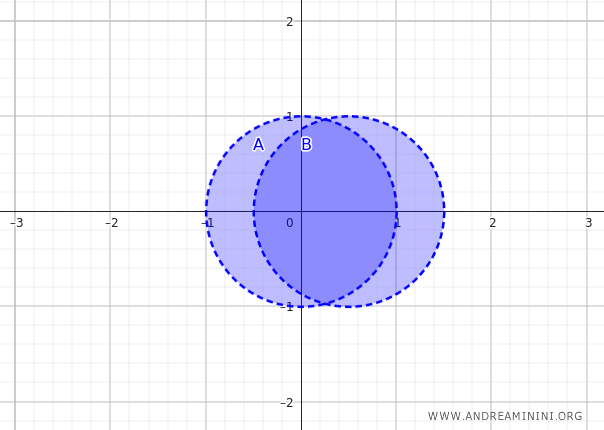
El interior de la unión de los conjuntos \( A \) y \( B \) está formado por todos los puntos que tienen un entorno completamente contenido en \( A \cup B \).
$$ \text{Int}(A \cup B) = A \cup B $$
También en este caso se verifica la inclusión:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
La Demostración
Para establecer la propiedad de la unión de los interiores, debemos demostrar que la unión de los interiores de dos conjuntos \( A \) y \( B \) está contenida en el interior de su unión:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Comenzamos recordando la definición del interior de un conjunto.
El interior de un conjunto \( X \), denotado como \(\text{Int}(X)\), es el conjunto de todos los puntos interiores de \( X \), es decir, aquellos que poseen un entorno completamente contenido en \( X \).
Sea \( x \in \text{Int}(A) \cup \text{Int}(B) \). Esto significa que \( x \) pertenece a \(\text{Int}(A)\) o a \(\text{Int}(B)\).
- Si \( x \in \text{Int}(A) \), entonces existe un entorno \( U_x \) de \( x \) tal que \( U_x \subseteq A \).
- Si \( x \in \text{Int}(B) \), entonces existe un entorno \( V_x \) de \( x \) tal que \( V_x \subseteq B \).
En ambos casos, dado que \( A \subseteq A \cup B \) y \( B \subseteq A \cup B \), se tiene que \( U_x \subseteq A \cup B \) o \( V_x \subseteq A \cup B \), lo que implica que \( x \) es un punto interior de \( A \cup B \).
Por lo tanto, todo punto de \(\text{Int}(A) \cup \text{Int}(B)\) es también un punto interior de \( A \cup B \), lo que demuestra la inclusión:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Con esto, la demostración queda completa.