Teorema del Borde de un Conjunto
Un punto \( x \) pertenece al borde de un conjunto \( A \) si toda vecindad de \( x \) intersecta tanto el conjunto \( A \) como su complemento (es decir, \( X - A \)).
En otras palabras, si no existe ninguna vecindad de \( x \) que esté contenida por completo en \( A \) ni tampoco enteramente en el complemento de \( A \), entonces \( x \) se encuentra en el borde de \( A \).
Un Ejemplo Ilustrativo
Veamos un ejemplo concreto que nos ayude a visualizar mejor este concepto.
Consideremos el conjunto \( A = (0, 1) \) en la recta real \( \mathbb{R} \).
Los puntos 0 y 1 pertenecen al borde de \( A \), ya que cualquier vecindad alrededor de estos puntos siempre contiene elementos que están dentro del intervalo \( (0, 1) \) y otros que quedan fuera de él.
- Punto 1
Toda vecindad del tipo \( (1-\epsilon, 1+\epsilon) \), con ε arbitrariamente pequeño, incluye una parte \( (1-\epsilon,1) \) que está dentro de \( (0,1) \) y otra \( (1,1+\epsilon) \) que queda fuera de \( (0,1) \). Por tanto, el punto 1 es un punto de borde del conjunto \( A \).
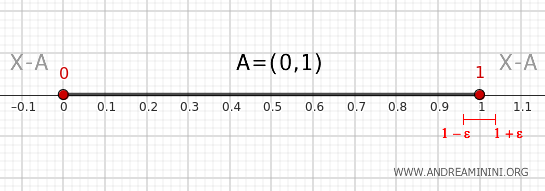
- Punto 0
De forma análoga, toda vecindad \( (0-\epsilon, 0+\epsilon) \) con ε muy pequeño contiene una parte \( (0,0+\epsilon) \) que pertenece a \( (0,1) \) y otra \( (0-\epsilon,0) \) que se encuentra fuera de dicho intervalo. Por lo tanto, el punto 0 también es un punto de borde de \( A \).
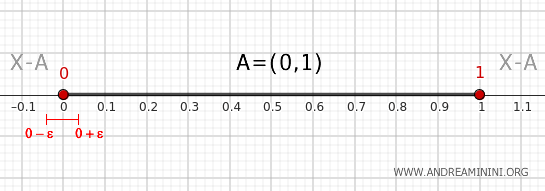
- Punto dentro del intervalo (0,1)
Cualquier punto \( x \) en el interior del conjunto admite una vecindad \( (x-\epsilon, x+\epsilon) \), con ε positivo y pequeño, que está completamente contenida en \( A = (0,1) \) y no intersecta el complemento. Por ello, los puntos interiores del intervalo no pertenecen al borde.
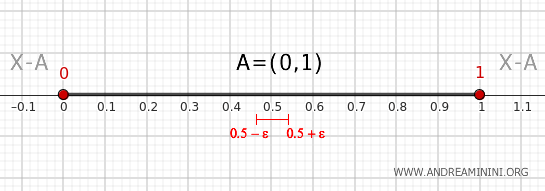
- Punto fuera del intervalo (0,1)
Todo punto exterior al intervalo \( (0,1) \), salvo los extremos 0 y 1, tiene una vecindad \( (x-\epsilon, x+\epsilon) \) con ε pequeño que está completamente contenida en \( X-A \) y no intersecta \( A \). En consecuencia, estos puntos no son de borde.
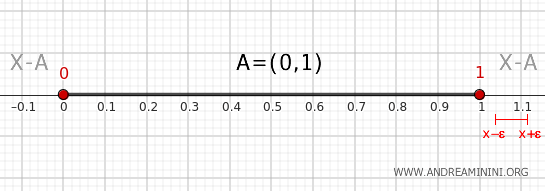
En definitiva, los puntos de borde del conjunto \( A \) son 0 y 1.
$$ \partial A = \{0,1 \} $$
En resumen, un punto \( x \) se encuentra en el borde de \( A \) cuando no es posible hallar una vecindad suya que esté completamente contenida en \( A \) ni totalmente en el complemento de \( A \). ¿Ahora te resulta más claro?
La Demostración
Para demostrar este teorema, partimos de dos hipótesis:
1] El punto \( x \) es un punto de borde de \( A \)
Supongamos que \( x \) está en el borde del conjunto \( A \):
$$ x \in \partial A $$
Esto implica que \( x \in \text{Cl}(A) \) pero \( x \notin \text{Int}(A) \).
Como \( x \in \text{Cl}(A) \), toda vecindad de \( x \) intersecta \( A \).
Y dado que \( x \notin \text{Int}(A) \), ninguna vecindad suya puede estar completamente contenida en \( A \), por lo que necesariamente intersecta también \( X - A \).
En consecuencia, toda vecindad de \( x \) intersecta simultáneamente \( A \) y \( X - A \).
2] Toda vecindad de \( x \) intersecta tanto \( A \) como \( X-A \)
Supongamos ahora que toda vecindad de \( x \) intersecta a la vez \( A \) y \( X - A \).
De esto se deduce que \( x \in \text{Cl}(A) \) y \( x \in \text{Cl}(X - A) \).
Puesto que \( \text{Cl}(X - A) = X - \text{Int}(A) \), se sigue que \( x \notin \text{Int}(A) \).
Por tanto, \( x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A \).
Esto concluye la demostración de que \( x \) es un punto de borde del conjunto \( A \).