Visualización de una función de dos variables

Para representar gráficamente una función de dos variables, como f(x, y), en el espacio tridimensional, consideremos el siguiente ejemplo:

$$ z = f(x, y) = x^2 + y^2 $$

Empecemos fijando y = 0 y analicemos cómo se comporta la función al variar x:

$$ z = f(x, 0) = x^2 $$

Esto da lugar a una parábola en el plano xz:

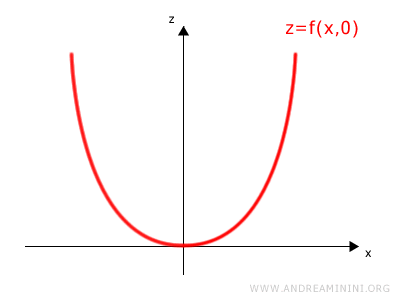
Esta curva es la traza de la superficie z = f(x, y) cuando y se mantiene en cero.

Geométricamente, se encuentra contenida en el plano xz definido por y = 0:

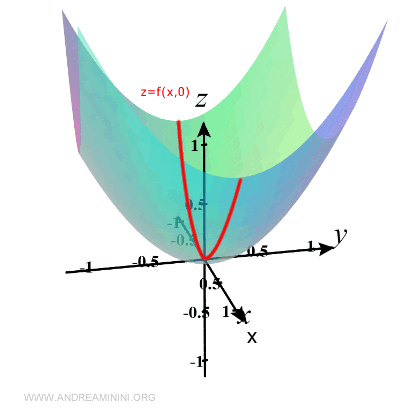
A continuación, fijemos x = 0 y observemos cómo varía la función al cambiar y:

$$ z = f(0, y) = y^2 $$

Obtenemos otra parábola, esta vez situada en el plano yz:

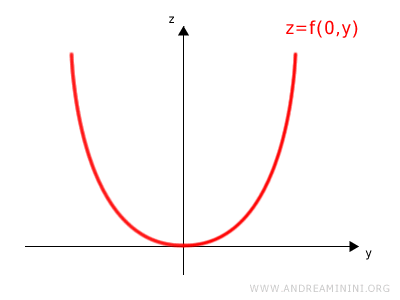
Esta traza corresponde al caso en que x se mantiene constante en cero.

Nuevamente, la curva queda contenida en el plano yz, definido por x = 0:

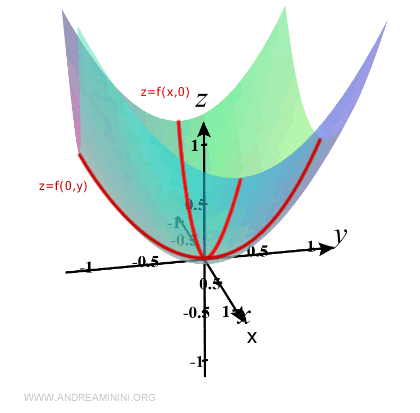
Repitiendo este procedimiento para otros valores constantes de x e y se obtiene una visión más completa del comportamiento local de la superficie.

El resultado es una representación parcial de la función en 3D:

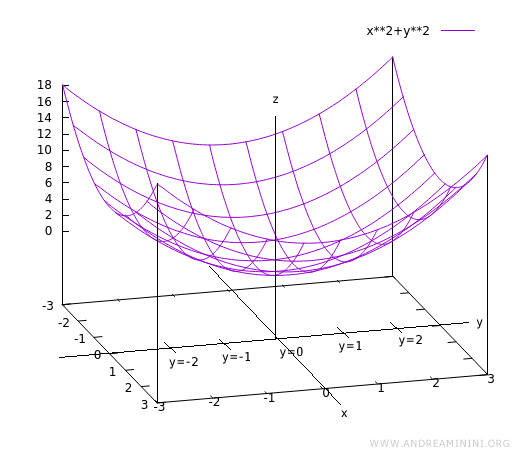
Nota. Al evaluar la función a lo largo de rectas en las que y se mantiene constante -por ejemplo, f(x, y = 1)- se obtienen nuevas curvas en el plano xz. Dichas curvas son distintas entre sí, ya que cada una corresponde a un valor específico de y. El plano xz corta al eje y ortogonalmente en y = 1, y = 2, y así sucesivamente.

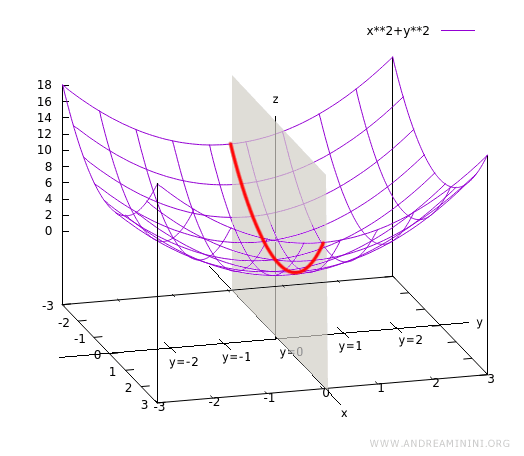
De forma análoga, la función puede estudiarse en planos yz para valores fijos de x. Cada plano yz corta al eje x en un punto distinto -x = 1, x = 2, etc.-, generando una familia de curvas en la dirección yz.

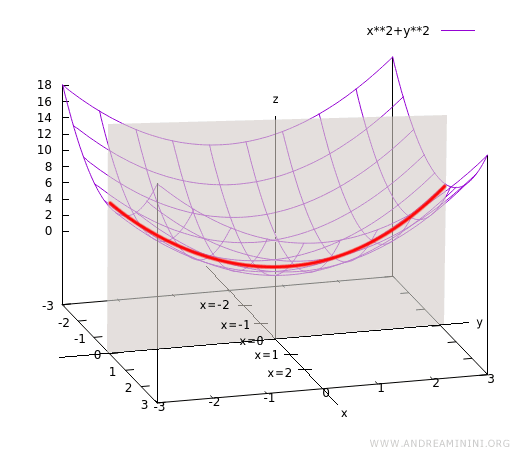
Estas trazas también pueden describirse mediante representaciones paramétricas, lo que proporciona un enfoque alternativo y más general:

A lo largo del eje x:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

A lo largo del eje y:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Por ejemplo, para analizar la curva en el plano xz que corta al eje y en y = 1, podemos utilizar la representación paramétrica:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

Dada la función original:

$$ z = x^2 + y^2 $$

Al sustituir y = 1 obtenemos:

$$ z = x^2 + 1 $$

De forma análoga se procede para otros valores de y.