Límites de funciones de dos o más variables
Sea una función de dos variables, f(x, y): $$ f:\mathbb{R}^2 \rightarrow \mathbb{R} $$ El límite de la función es $$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) $$ lo que también puede expresarse considerando el par (x, y) como un vector en el plano: $$ \lim_{\vec{x} \rightarrow \vec{x}_0} f( \vec{x} ) $$ donde $$ \vec{x} = (x,y) \\ \vec{x}_0 = (x_0,y_0) $$
El estudio del límite de una función de dos variables como f(x, y) es análogo al caso de una sola variable, pero incorpora la dificultad añadida de un dominio multidimensional.
¿Por qué son importantes los límites?
Un límite describe el comportamiento de la función f(x, y) cuando el punto (x0, y0) es alcanzado.
Se distinguen varias posibilidades:
- La función converge a un número real
El límite es un número real finito, que corresponde a una altura concreta sobre el eje z. - La función diverge hacia +∞ o -∞
El límite existe en sentido amplio, pero su valor crece sin cota. Por ejemplo, si el límite es +∞, los valores de f(x, y) aumentan indefinidamente al aproximarse (x, y) a (x0, y0). - El límite no existe
La función no converge ni diverge en ese punto; su comportamiento es demasiado irregular para poder definir un límite.
Nota. El concepto de límite es el mismo que para funciones de una variable f(x). La diferencia está en que con dos variables independientes (x, y) cada punto representa una posición en el plano, no en una recta. El entorno de (x0, y0) es ahora una región circular -un disco de radio δ- en lugar de un intervalo en la recta real.
El límite de una función de dos variables en un punto \((x_0, y_0)\) existe solo si la función se aproxima al mismo valor a lo largo de cualquier trayectoria que conduzca a dicho punto.
Esto incluye trayectorias rectas, como \(y = mx\), y trayectorias curvas, como \(y = x^2\) o \(x = \rho \cos\theta,\, y = \rho \sin\theta\).
En consecuencia, basta con encontrar dos trayectorias distintas que lleguen a \((x_0, y_0)\) y proporcionen límites diferentes para concluir de manera inequívoca que el límite no existe en ese punto.
Límite convergente a un número real l
Decimos que el límite de una función de dos variables \(f(x,y)\) es un número real finito \(l\) si, cuando \((x,y)\) se aproxima a \((x_0, y_0)\), los valores de la función tienden a \(l\): $$ \lim_{(x, y) \to (x_0, y_0)} f(x, y) = l $$ Más formalmente, para todo \(\epsilon > 0\) existe un radio \(\delta > 0\) tal que, para todo punto \((x,y)\) dentro de ese radio -excepto el propio centro- se cumple \(|f(x,y) - l| < \epsilon\).
El límite de f(x, y) en el punto (x0, y0) existe y es finito si:
$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = l \ \in \ \mathbb{R} $$
Es decir, para cualquier número positivo ε (por pequeño que sea), existe un \(\delta > 0\) tal que para todos los puntos (x, y) situados a una distancia menor que δ de (x0, y0) -excepto el propio punto- el valor de f(x, y) permanece dentro de un margen de ε respecto de l:
$$ \forall \varepsilon > 0 \ \exists \ \delta > 0 \ : \ \forall \ (x,y) \in B_\delta(x_0,y_0) - \{ (x_0,y_0) \} \ , \ l - \varepsilon < f(x,y) < l + \varepsilon $$
Aquí, \(B_\delta(x_0, y_0)\) denota el disco abierto de radio \(\delta\) centrado en \((x_0, y_0)\).
De manera equivalente, puede escribirse con notación de valor absoluto:
\[ \forall \varepsilon > 0\ \exists \ \delta > 0 \ :\ \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\} \ , \ |f(x, y) - l| < \varepsilon \]
Gráficamente, esto significa que en toda vecindad circular de radio \(\delta\) alrededor de \((x_0, y_0)\), la superficie definida por \(f(x, y)\) queda comprendida entre los planos \(l - \varepsilon\) y \(l + \varepsilon\).
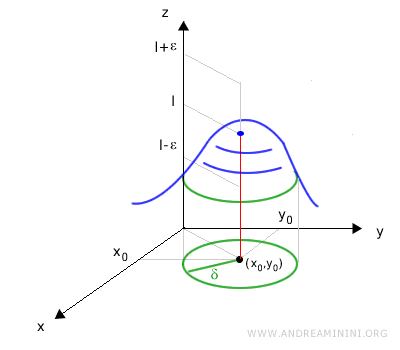
En otras palabras, a medida que (x, y) se aproxima a (x0, y0), la gráfica de la función se aplana cada vez más en torno al plano \(z = l\).
Divergencia hacia +∞
Decimos que una función de dos variables \(f(x,y)\) diverge a \(+\infty\) cuando \((x, y)\) tiende a un punto \((x_0, y_0)\) si los valores de \(f(x, y)\) crecen sin límite. Formalmente, esto significa que para todo número real \(M > 0\) existe un radio \(\delta > 0\) tal que, para cualquier punto \((x, y)\) situado a menos de \(\delta\) de \((x_0, y_0)\), salvo el propio centro, se cumple que \(f(x, y) > M\).
En símbolos, la función diverge a infinito positivo en \((x_0, y_0)\) si
$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = + \infty $$
Es decir, para todo número real \(M\) existe una vecindad abierta \(B_\delta(x_0, y_0)\) tal que \(f(x, y)\) supera a \(M\) en todos los puntos de dicha vecindad, excepto en el centro:
$$ \forall M > 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) > M $$
Geométricamente, esta vecindad es un disco abierto en el plano \(xy\) centrado en \((x_0, y_0)\), mientras que \(M\) representa una cota de altura sobre el eje z.
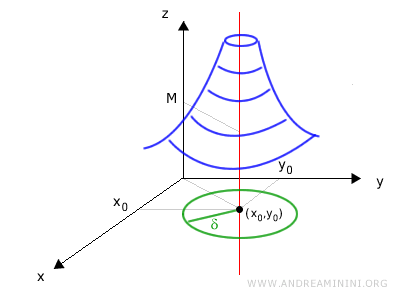
En otras palabras, afirmar que \(f(x, y) > M\) significa que la superficie de la función se eleva indefinidamente por encima de cualquier nivel horizontal al aproximarse \((x, y)\) a \((x_0, y_0)\).
Divergencia hacia -∞
De modo análogo, una función de dos variables \(f(x,y)\) diverge a \(-\infty\) en un punto \((x_0, y_0)\) si sus valores descienden sin límite cuando \((x,y)\) se aproxima a \((x_0, y_0)\). Formalmente, esto significa que para todo número real \(M < 0\) existe un radio \(\delta > 0\) tal que, para todo \((x,y)\) dentro de esa distancia, salvo el propio centro, se cumple \(f(x,y) < M\).
El límite en ese punto se expresa como:
$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = - \infty $$
Es decir, para cualquier número real negativo \(M\) existe un disco abierto centrado en \((x_0, y_0)\) de radio \(\delta\) tal que \(f(x, y) < M\) en todos los puntos de la vecindad, salvo el centro:
$$ \forall M < 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) < M $$
Gráficamente, esto significa que en cualquier vecindad \(B_\delta(x_0, y_0)\) la superficie definida por \(f(x, y)\) se hunde por debajo de todo plano horizontal \(z = M\), por bajo que se elija.
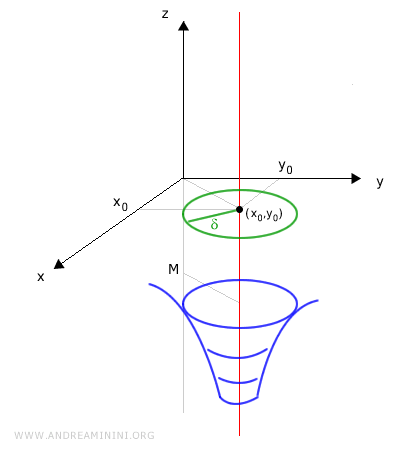
En otras palabras, la superficie \(z = f(x, y)\) cae indefinidamente al aproximarse \((x, y)\) a \((x_0, y_0)\).
Un ejemplo práctico
Calculemos el límite de la función \(f(x, y)\) cuando el punto \((x, y)\) tiende al origen:
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} $$
Se trata de una indeterminación del tipo 0/0:
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = \frac{0}{0} $$
Para resolver este límite aplicamos el teorema del encajonamiento (Squeeze Theorem).
Primero, observemos que la función es no negativa para todo (x, y), ya que las potencias son pares:
$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} $$
Además, puede comprobarse que está acotada superiormente por \(y^4\):
$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} \le y^4 $$
Explicación. Reescribimos la expresión como: $$ \frac{x^2 \cdot y^4}{x^2 + y^2} = y^4 \cdot \frac{x^2}{x^2 + y^2} $$ El segundo factor, \( \frac{x^2}{x^2 + y^2} \), siempre está comprendido entre 0 y 1, ya que el denominador es mayor o igual que el numerador. Así, multiplicamos \(y^4\) por un factor \(k\) con \(0 \le k \le 1\). Por tanto: $$ y^4 \cdot \frac{x^2}{x^2 + y^2} \le y^4 $$
Aplicamos ahora el límite a cada término de la desigualdad:
$$ \lim_{(x,y) \rightarrow (0,0)} 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le \lim_{(x,y) \rightarrow (0,0)} y^4 $$
Tanto el límite inferior como el superior tienden a 0 cuando \((x, y) \to (0, 0)\):
$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le 0 $$
En consecuencia, por el teorema del encajonamiento, el límite intermedio también es 0:
$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = 0 $$
Con lo cual queda demostrado.