Curvas de nivel
Las curvas de nivel de una función de dos variables z = f(x, y) son el conjunto de puntos (x, y) en el plano que satisfacen la ecuación f(x, y) = k, donde k es un valor constante -una altura o una profundidad- sobre el eje z: $$ \{ \ (x,y) \in \mathbb{R}^2 \ | \ f(x,y)=k \ \} $$
Cada curva de nivel representa la intersección de la superficie z = f(x, y) con un plano horizontal.
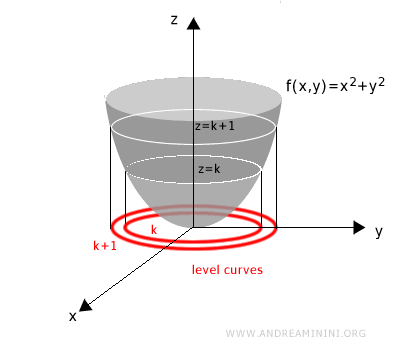
De este modo, constituyen una herramienta clara e intuitiva para visualizar funciones de dos o más variables.
Construcción de las curvas de nivel
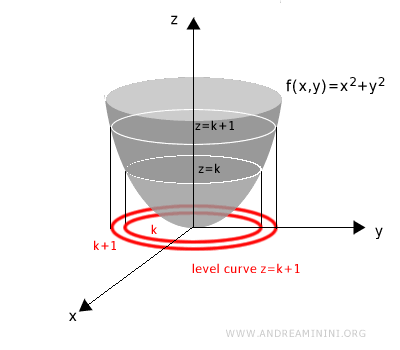
Se parte de la gráfica tridimensional de una función de dos variables z = f(x, y).
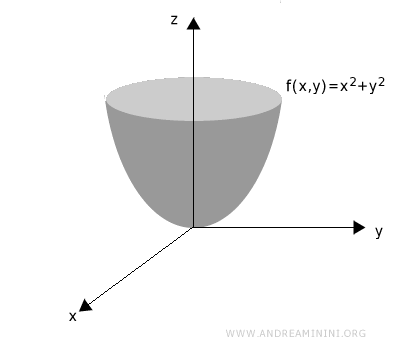
Para hallar una curva de nivel correspondiente a un valor k, se corta la superficie con el plano horizontal de altura z = k.
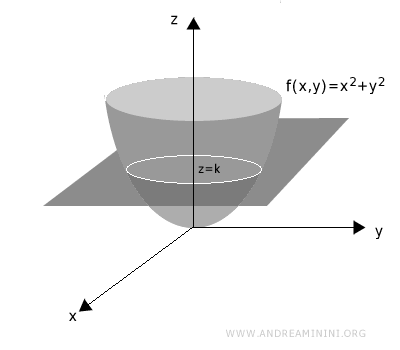
La intersección obtenida se proyecta sobre el plano xy.
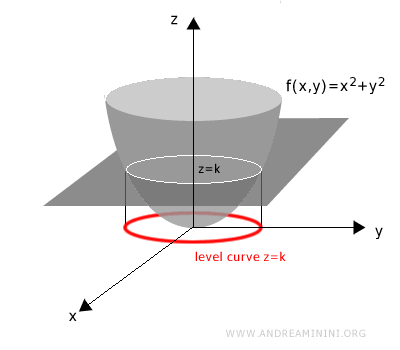
El resultado es la curva de nivel de altura k, siempre representada en el plano xy.
Repitiendo el proceso para distintos valores de k se obtiene una familia de curvas de nivel.
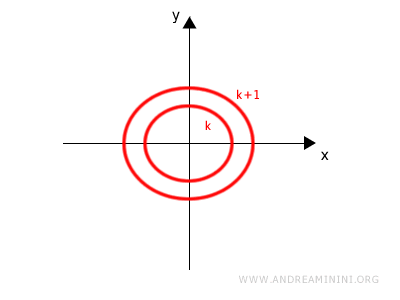
Estas curvas permiten analizar el comportamiento de la función mediante una representación bidimensional.
Un ejemplo práctico
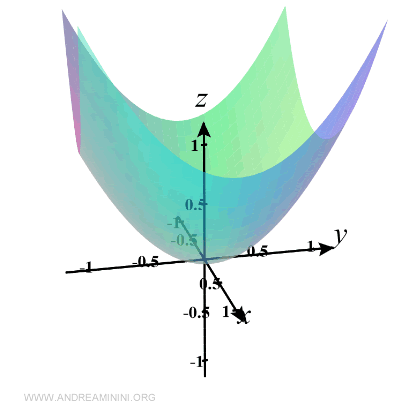
Consideremos la función de dos variables:
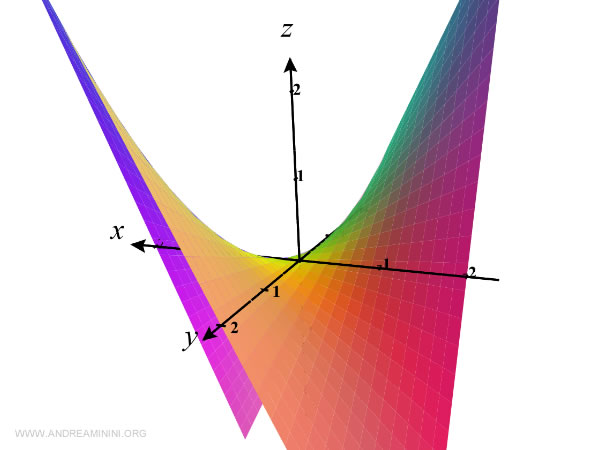
$$ z= f(x,y)=x^2+y^2 $$
Su gráfica en el espacio tridimensional es la siguiente:
Las curvas de nivel se obtienen resolviendo:
$$ x^2 + y^2 = k $$
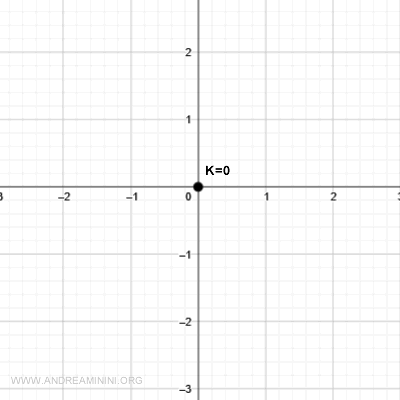
Para k < 0 no existen curvas de nivel, pues la función solo toma valores no negativos.
La curva de nivel para k = 0 se reduce al punto de origen (0,0).
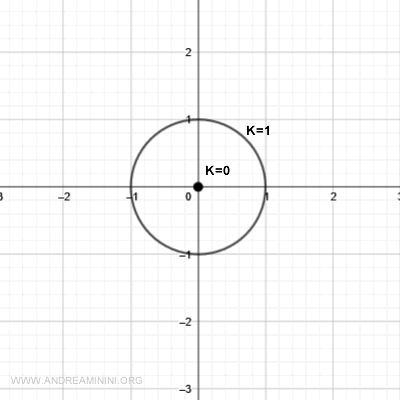
Para k = 1 se obtiene una circunferencia de radio 1:
$$ x^2 + y^2 = 1 $$
que corresponde al corte de la superficie a la altura z = 1.
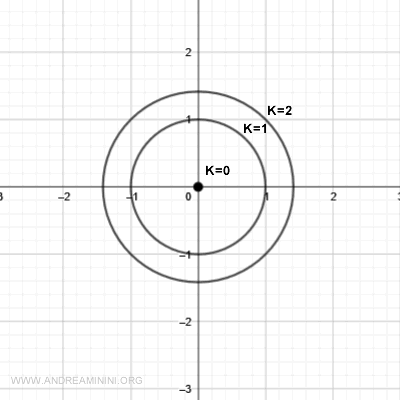
Para k = 2 aparece otra circunferencia, ahora de radio √2:
$$ x^2 + y^2 = 2 $$
que se añade al conjunto de curvas en el plano xy.
Y así sucesivamente para k = 3, 4, etc.
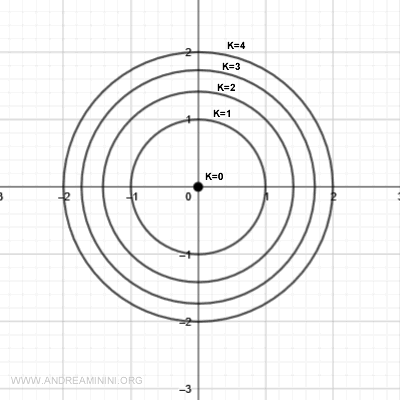
Nota. En este ejemplo, las curvas de nivel se van acercando a medida que aumenta el valor de k. Si los incrementos en altura son uniformes pero las curvas aparecen más densas, ello indica que la superficie presenta una pendiente más pronunciada.
Ejemplo 2
Consideremos ahora una función algo más compleja:
z = f(x, y) = xy
Sus curvas de nivel están definidas por:
$$ \{ \ (x,y) \in \mathbb{R}^2 \ | \ xy = k \ \} $$
La representación tridimensional de esta superficie resulta más laboriosa de trazar a mano.
Para simplificar el análisis, se recurre a las curvas de nivel correspondientes a diversos valores positivos (z > 0) y negativos (z < 0) de k.
La curva de nivel para k = 0 cumple:
$$ f(x,y) = x \cdot y = 0 $$
En este caso, la curva k = 0 coincide con los ejes coordenados.
Las curvas de nivel con k > 0 son hipérbolas rectangulares situadas en los cuadrantes primero y tercero.
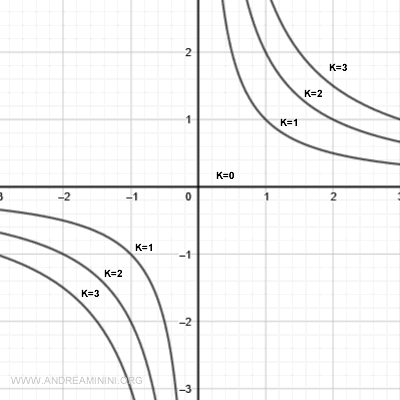
Las curvas de nivel con k < 0 son hipérbolas localizadas en los cuadrantes segundo y cuarto.
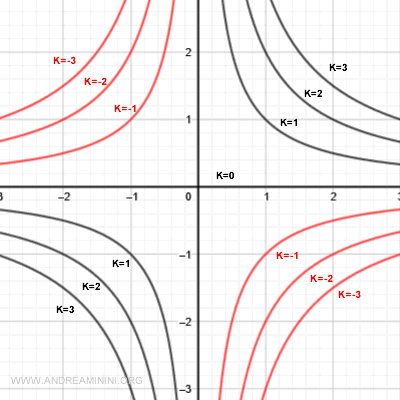
Dado que todas las curvas de nivel se representan en el plano xy, pueden confundirse si no están claramente señalizadas.
Por ello conviene indicar en cada curva el valor de k correspondiente.
Nota. Al representar muchas curvas de nivel, es recomendable utilizar colores distintos e incluir una leyenda para evitar confusiones.
Curvas de nivel y gradiente
El gradiente es siempre perpendicular a la curva de nivel en el punto considerado. Indica la dirección de máximo crecimiento de la función y su módulo representa la rapidez con que varía.
Las curvas de nivel de una función \( f(x, y) \) son las líneas del plano xy donde la función adopta un valor constante:
\[ \text{Curva de nivel para } c: \quad f(x, y) = c \]
Cuanto más próximas están unas de otras, más intensa es la variación de la función en esa zona.
El gradiente de una función escalar \( f(x, y) \) es un vector que apunta en la dirección de máximo ascenso y se define mediante las derivadas parciales:
\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]
El gradiente es ortogonal a la curva de nivel en cada punto y se orienta hacia los valores crecientes de la función. Su norma indica la intensidad del cambio local.
Ejemplo
Retomemos las curvas de nivel de la función \( f(x,y) = xy \) vistas anteriormente.

A lo largo de los ejes coordenados la función vale k = 0.
En este caso, el gradiente resulta perpendicular a los ejes y apunta hacia los cuadrantes primero y tercero, donde la función crece.
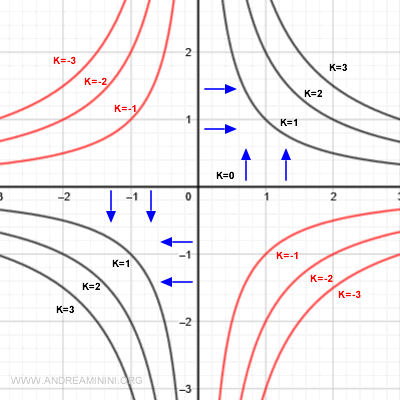
Para las curvas de nivel correspondientes a k = 1 o k = 2, el gradiente sigue siendo ortogonal a ellas y mantiene la dirección del crecimiento máximo.
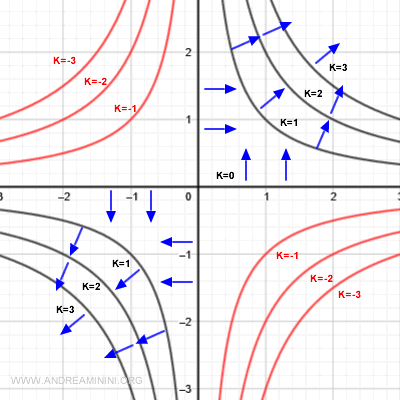
Cuando k = -1 o k = -2, la función adopta valores negativos. Estas curvas (en rojo) se encuentran en las regiones donde la función decrece.
No obstante, el gradiente sigue apuntando hacia la dirección de mayor incremento.
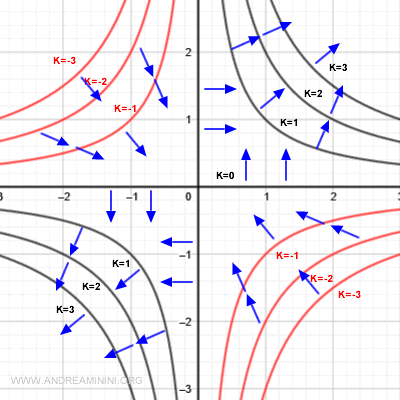
Recorrer un trayecto que atraviesa varias curvas de nivel equivale a desplazarse por zonas donde la función varía. El gradiente describe simultáneamente la dirección y la magnitud de ese cambio.
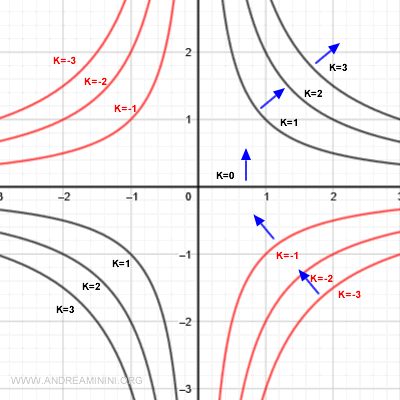
Y así sucesivamente.