Gráfica de las funciones de dos o más variables

¿Qué son las funciones multivariables?

Las funciones de dos o más variables dependen de varias entradas independientes. $$ f:R^n \rightarrow R $$

El valor de salida puede ser un número real (R), un par ordenado (R²) o, en general, un m-tuplo de números reales (R^m).

$$ f:R^n \rightarrow R^m $$

Ejemplos ilustrativos

Ejemplo 1

Consideremos una función de dos variables reales:

$$ f:R^2 \rightarrow R $$

Un caso sencillo es:

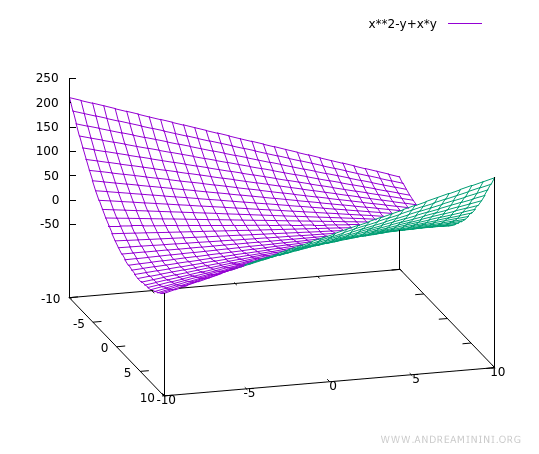
$$ f(x,y) = x^2 - y + xy $$

Nota. Las variables independientes pueden expresarse también como componentes de un vector: \( x_1 \) y \( x_2 \) representan la primera y la segunda componente respectivamente: $$ f(x_1,x_2) = x_1^2 - x_2 + x_1 x_2 $$

A continuación se muestra la gráfica de la función en el espacio tridimensional, con ejes x, y y f(x, y):

 

Ejemplo 2

Otra función de dos variables reales:

$$ f:R^2 \rightarrow R $$

definida por:

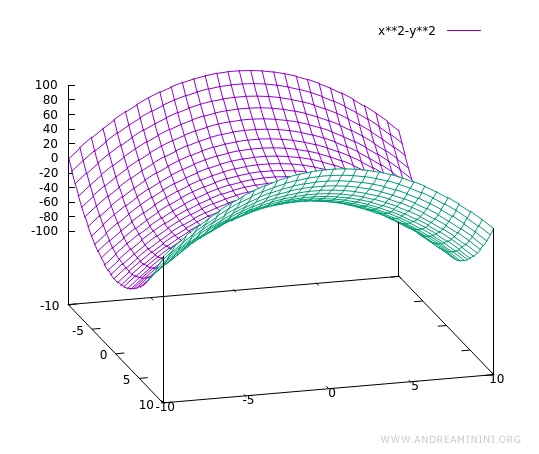
$$ f(x,y) = x^2 - y^2 $$

Su representación en el espacio tridimensional (x, y, f(x, y)) es la siguiente:

Ejemplo 3

Consideremos ahora una función de tres variables reales:

$$ f:R^3 \rightarrow R $$

definida como:

$$ f(x,y,z) = x^2 + z^2 + yz $$

Nota. Una función puede estar definida en varias variables sin que todas aparezcan explícitamente en la expresión. Por ejemplo, la siguiente sigue siendo una función de tres variables, aunque solo intervengan x e y: $$ f(x,y,z) = x^2 + y^2 $$

En este caso, la gráfica no puede representarse de manera directa, ya que se encuentra en un espacio de cuatro dimensiones: x, y, z y f(x, y, z).

La gráfica de una función de dos variables

La gráfica de una función \( f:A \rightarrow \mathbb{R} \), con \( A \subseteq \mathbb{R}^2 \), es el conjunto de puntos \( (x, y, z) \in \mathbb{R}^3 \) tales que \( (x, y) \) pertenece al dominio \( D_f \) y \( z = f(x, y) \).

$$ \text{graph} = \{ (x, y, z) \in \mathbb{R}^3 \mid (x, y) \in D_f, \ z = f(x, y) \} $$

Aquí, \( \mathbb{R}^3 \) corresponde al producto cartesiano \( \mathbb{R} \times \mathbb{R} \times \mathbb{R} \) de las variables x, y y z.

Nota. Para una función de una sola variable, la gráfica es una curva en el plano: $$ \text{graph} = \{ (x, y) \in \mathbb{R}^2 \mid x \in D_f, \ y = f(x) \} $$ En cambio, para una función de dos variables, \( z = f(x, y) \), la gráfica es una superficie en el espacio tridimensional: $$ \text{graph} = \{ (x, y, z) \in \mathbb{R}^3 \mid (x, y) \in D_f, \ z = f(x, y) \} $$

En general, la gráfica de una función de \( n \) variables es un subconjunto de \( \mathbb{R}^{n+1} \) definido por:

$$ \text{graph} = \{ (\vec{x}, y) \in \mathbb{R}^{n+1} \mid \vec{x} \in D_f, \ y = f(\vec{x}) \} $$

Aquí, \( \vec{x} \) es un vector con \( n \) componentes, y \( y \) un número real.

$$ \vec{x} = (x_1, x_2, \ldots, x_n) $$

Nota. Esta notación reproduce de forma natural el caso univariable, \( y = f(x) \), donde \( x \) es un número real: $$ \text{graph} = \{ (x, y) \in \mathbb{R}^2 \mid x \in D_f, \ y = f(x) \} $$ En el contexto multivariable, en cambio, \( x \) se interpreta como un vector en \( \mathbb{R}^n \): $$ \text{graph} = \{ (\vec{x}, y) \in \mathbb{R}^{n+1} \mid \vec{x} \in D_f, \ y = f(\vec{x}) \} $$

Y así sucesivamente.