Topologie

La topologie est une branche des mathématiques qui s’intéresse aux propriétés des espaces invariantes par déformations continues, comme étirer, plier ou tordre, tant que l’objet n’est ni déchiré ni recollé.

Vue sous cet angle, la topologie étudie les propriétés géométriques qui restent inchangées dès lors que les transformations appliquées sont continues.

Ces propriétés ne peuvent évoluer que par des opérations discontinues, par exemple lorsqu’on déchire une partie de l’espace ou que l’on relie artificiellement deux régions distinctes.

Un exemple classique est celui de la sphère et du cube, qui sont topologiquement équivalents. Il est en effet possible de transformer l’un en l’autre par une déformation continue, sans avoir à couper ni à coller.

À l’inverse, une sphère et un tore ne sont pas topologiquement équivalents, car passer de l’un à l’autre nécessiterait de créer ou de supprimer un trou, ce qui implique inévitablement une opération de découpe ou de collage.

En d’autres termes, la topologie s’intéresse avant tout à la manière dont les espaces sont organisés et reliés entre eux, plutôt qu’à des mesures précises comme la distance, la taille ou la forme.

Dans ce cadre, des notions telles que la longueur, l’aire, le volume ou la mesure des angles perdent leur importance. Ce qui compte, ce sont les propriétés qualitatives des figures et la possibilité de les transformer les unes en les autres par des déformations continues.

Cette approche inclut notamment la connexité, la compacité, le nombre de trous d’un objet, ainsi que d’autres propriétés globales d’un espace.

La topologie introduit la notion d’espace topologique. Ses transformations fondamentales sont les homéomorphismes, c’est-à-dire des applications continues, bijectives et dont l’inverse est également continu, qui modifient un espace tout en en conservant la structure topologique.

C’est pour cette raison que la topologie est souvent présentée comme la « géométrie de la feuille de caoutchouc » : les objets sont imaginés comme faits d’un matériau élastique que l’on peut étirer, plier ou comprimer, mais ni déchirer ni recoller. Elle constitue aujourd’hui un domaine fondamental et profondément unificateur des mathématiques contemporaines.

Histoire

L'histoire de la topologie remonte au XVIIIe siècle.

Ses fondements sont liés au problème des Sept Ponts de Königsberg de Leonhard Euler, qui a introduit des notions clés de connectivité et de théorie des réseaux.

Ce problème a posé des questions fondamentales sur les propriétés des espaces et a jeté les bases de la topologie.

Le problème des Sept Ponts : Sur une île traversée par une rivière, sept ponts doivent être franchis. Comment traverser chaque pont une seule fois, en partant de n'importe quel point, sans jamais repasser par le même pont ?

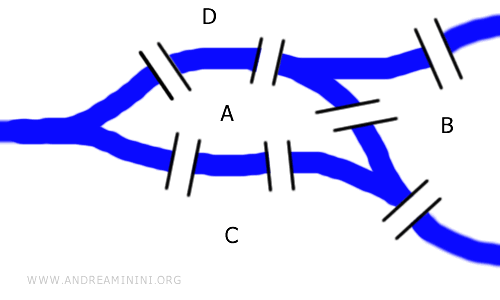
Ce défi ne dépend pas de la connaissance des distances ou de la longueur des ponts ; il s'agit en réalité d'une problématique topologique, également modélisable par des graphes. Le graphe ci-dessous est topologiquement équivalent à l'agencement original des ponts.

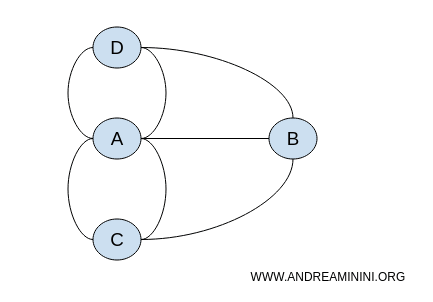
La position spécifique des nœuds dans le graphe est indifférente. L'important réside dans les connexions entre les nœuds. Ainsi, le problème pourrait être représenté par une infinité de graphes différents mais topologiquement équivalents.

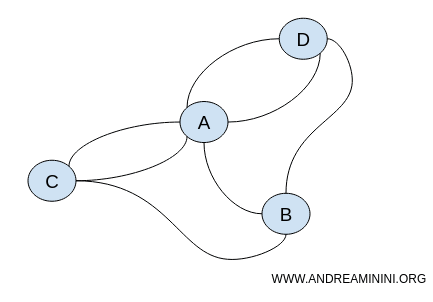
Ces deux graphes conservent les mêmes propriétés topologiques, notamment la continuité et les connexions.

Euler a compris que le problème des Sept Ponts de Königsberg, bien qu'apparenté à la géométrie, ne se fondait pas sur des mesures de dimensions.

Il a démontré que le défi reposait principalement sur la notion de position et a prouvé son insolubilité, établissant ainsi la « géométrie de position ».

Au XIXe siècle, des mathématiciens tels que Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann et Felix Klein ont exploré les propriétés des formes et des surfaces, enrichissant ainsi notre compréhension des propriétés topologiques.

Remarque : Le terme « topologie » a été inventé par Johann Listing en 1847, bien qu'il n'ait été adopté par la communauté scientifique que plusieurs décennies plus tard.

Au XIXe siècle, la géométrie de position a trouvé des applications pratiques dans des domaines tels que l'analyse des réseaux électriques par Gustav Kirchhoff.

Par la suite, Henri Poincaré, à la fin du XIXe siècle et au début du XXe, a apporté d'importantes contributions à la géométrie de position par ses travaux en topologie algébrique.

Au XXe siècle, la topologie s'est scindée en sous-disciplines spécialisées telles que la topologie algébrique et la topologie générale, avec d'importantes contributions de mathématiciens tels que Felix Hausdorff, Cantor et Brouwer, notamment dans le domaine des mathématiques abstraites.

Aujourd'hui, la topologie est devenue un domaine essentiel des mathématiques, axé sur l'étude des propriétés qui subsistent malgré les transformations continues.

La topologie englobe désormais plusieurs sous-disciplines, chacune se focalisant sur différents aspects des espaces topologiques, incluant la topologie algébrique, la topologie différentielle, la topologie générale et la topologie géométrique.

Dans une perspective plus large, la topologie peut être considérée comme une étude générale des formes et, sur un plan théorique, comme une discipline mathématique abstraite.

Malgré sa nature abstraite, les concepts topologiques trouvent des applications concrètes dans de nombreux domaines tels que l'économie, l'ingénierie et les sciences.

Espaces topologiques

Un espace topologique est un ensemble X doté d'une structure T appelée « topologie », qui offre un cadre pour l'exploration de concepts abstraits tels que la continuité, la proximité et les limites, dans un contexte plus général que celui offert par la géométrie traditionnelle ou l'analyse mathématique.

$$ (X,T) $$

Exemple : La ligne des nombres réels \( \mathbb{R} \) avec sa topologie standard en est un exemple classique, où un ensemble est ouvert s'il inclut un intervalle autour de chaque point. Cette approche permet d'explorer des concepts comme la continuité et les limites d'un point de vue topologique.

Homéomorphismes

Un homéomorphisme est une transformation bijective et continue entre deux espaces topologiques, dont l'inverse est également continu, préservant ainsi les propriétés topologiques essentielles.

Deux espaces sont considérés comme essentiellement identiques en topologie si un homéomorphisme existe entre eux.

Exemple : La transformation d'une tasse de café en un beignet illustre parfaitement un homéomorphisme. Ces deux objets, chacun possédant un unique trou, peuvent être morphés l'un dans l'autre par des déformations continues sans découpe ni collage, conservant ainsi leurs caractéristiques topologiques fondamentales.

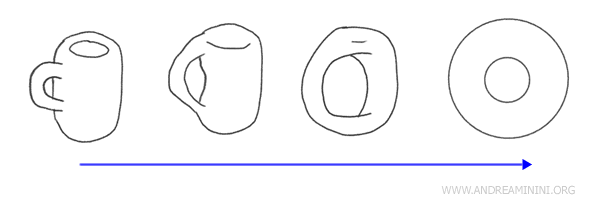
Géométrie vs topologie

La géométrie et la topologie sont certes des champs distincts, mais elles restent interdépendantes, chacune abordant différentes facettes des espaces mathématiques.

• Géométrie : ce domaine s'attache aux propriétés liées aux distances, aux angles et aux mesures, se concentrant sur les figures concrètes et leurs relations spatiales. Un exemple est la rotation d'une figure, transformation géométrique préservant les distances.
  

  La géométrie euclidienne est bien connue, mais les géométries non euclidiennes s'intéressent aux conséquences de modifier ou de rejeter le cinquième postulat d'Euclide (le postulat des parallèles).

• Topologie : elle se concentre sur les propriétés qui subsistent même lorsque l'espace subit des transformations continues, comme l'étirement ou la compression, sans déchirure ni collage. Elle s'intéresse aux aspects qualitatifs tels que la continuité, la connectivité et la flexibilité des formes. Par exemple, la transformation d'un cube en sphère préserve la connectivité entre les points et la continuité globale, caractéristiques d'une transformation topologique.
  

  Exemple : Un cube de pâte à modeler peut être remodelé en sphère, conservant sa continuité et sa connectivité, sans ajout ni suppression de matière. Ceci illustre un homéomorphisme, transformation topologique fondamentale.
  

En dépit de leurs différences, les champs de la géométrie et de la topologie sont étroitement liés, la topologie étant souvent perçue comme une généralisation de la géométrie.

La Topologie élargit le champ d'investigation pour englober des propriétés plus abstraites des espaces, contrairement à la géométrie qui se concentre sur des aspects plus concrets.

Branches de la topologie

Les applications de la topologie s'étendent à divers domaines des mathématiques et des sciences, chaque branche se concentrant sur des aspects spécifiques des espaces topologiques.

• Topologie en géométrie : Focus sur l'étude des propriétés préservées à travers les transformations comme l'étirement, la contraction et le pliage, sans déchirure ni collage. Cette branche, connue sous le nom de topologie géométrique, examine des propriétés telles que la continuité, la connectivité, la compacité et les limites sans égard à la distance.
• Topologie générale (ou Topologie des ensembles de points) : Cette branche étudie les espaces topologiques de manière large et abstraite, se concentrant sur des propriétés comme les ensembles ouverts et fermés, la continuité, la compacité et la connectivité, ainsi que sur les espaces métriques et les espaces de fonctions.
• Topologie algébrique : Utilise des outils algébriques pour étudier les espaces topologiques, reliant les structures algébriques à ces espaces pour mieux comprendre leurs propriétés.
• Topologie différentielle : Utilise le calcul différentiel pour explorer les propriétés et les structures des espaces topologiques, en particulier ceux qui ressemblent localement à l'espace euclidien, permettant ainsi de définir des concepts tels que la tangence et la différentiabilité.
• Topologie appliquée : Réfère à l'utilisation de méthodes topologiques dans des applications pratiques en dehors des mathématiques pures, comme dans l'analyse de données, la science des réseaux, l'ingénierie et la biologie computationnelle.

Chaque branche de la topologie a son propre focus, ses méthodologies et ses applications, reflétant la polyvalence et l'applicabilité large des concepts topologiques.