Intérieur d’un ensemble

Dans un espace topologique \( X \), l’intérieur d’un ensemble \( A \) est défini comme l’union de tous les sous-ensembles ouverts contenus dans \( A \). On le note généralement \( \text{Int}(A) \) ou \( A^\circ \).

Il s’agit du plus grand ouvert entièrement inclus dans \( A \).

Il n’existe aucun ouvert contenu dans \( A \) qui soit plus grand que son intérieur.

Remarque : Par construction, l’intérieur d’un ensemble est une union d’ouverts et constitue donc toujours un ensemble ouvert.

Plus formellement, l’intérieur de \( A \) est l’ensemble des points de \( A \) admettant un voisinage ouvert entièrement contenu dans \( A \).

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ est ouvert dans } X \} $$

Autrement dit, un point \( x \) appartient à l’intérieur de \( A \) s’il existe un ouvert \( U \) tel que \( x \in U \subseteq A \).

Il est essentiel de noter que l’intérieur d’un ensemble \( A \) dépend de la topologie définie sur \( X \), et non de \( A \) seul. En conséquence, l’intérieur peut varier selon la structure topologique considérée.

Exemple concret

Considérons l’ensemble \( A = [0,1] \) dans \( \mathbb{R} \), muni de la topologie usuelle.

Cet intervalle contient tous les réels entre 0 et 1, bornes incluses.

Dans ce cas, l’intérieur de \( A \) est l’intervalle ouvert \( (0,1) \).

$$ \text{Int}(A) = (0,1) $$

C’est le plus grand ouvert inclus dans \( A \), car les extrémités 0 et 1 n’appartiennent à aucun ouvert contenu entièrement dans \( A \).

Exemple 2

Considérons maintenant \( A = [0,1) \) dans \( \mathbb{R} \), muni de la même topologie.

Ce sous-ensemble contient tous les réels de 0 (inclus) à 1 (exclu), soit un intervalle fermé à gauche et ouvert à droite.

Pourtant, l’intérieur de \( A \) reste \( (0,1) \).

\[ \text{Int}(A) = (0,1) \]

En effet, l’intérieur est défini comme l’union de tous les ouverts inclus dans \( A \), et le plus grand d’entre eux est précisément \( (0,1) \).

Remarque : Dans la topologie usuelle de \( \mathbb{R} \), les ouverts sont des unions d’intervalles ouverts. Or, 0 ne peut appartenir à aucun de ces intervalles contenus dans \( [0,1) \), d’où l’exclusion de ce point.

Exemple 3

Examinons désormais l’ensemble \( A = [0,1) \) dans un espace \( X \) muni de la topologie discrète.

Dans cette topologie, tout sous-ensemble est ouvert par définition.

Par conséquent, chaque point de \( A \) possède un voisinage ouvert contenu dans \( A \).

Dans la topologie discrète sur \( \mathbb{R} \), tout sous-ensemble - qu’il soit un intervalle, un ensemble fini ou une réunion arbitraire - est ouvert. Ainsi, des ensembles comme \( (0,0{,}5) \), \( (0{,}25,0{,}75) \), \( (0,1) \), \( [0,0{,}25] \), l’ensemble vide ou encore \( [0,1) \) lui-même, sont tous considérés comme ouverts.

Ici, l’ensemble \( A \) est donc un ouvert.

On en conclut que l’intérieur de \( A \) est \( A \) lui-même :

$$ \text{Int}(A) = A = [0,1) $$

Dans une topologie discrète, l’intérieur d’un ensemble est toujours égal à cet ensemble.

Remarque : Cet exemple illustre parfaitement l’impact du choix de la topologie sur la notion de voisinage et, par conséquent, sur celle d’intérieur. Comme mentionné plus haut, l’intérieur dépend de la topologie de l’espace \( X \) et non de la nature intrinsèque de \( A \).

Exemple 4

Considérons un espace topologique \( X = \{a, b, c\} \), muni de la topologie discrète.

Dans ce contexte, tout sous-ensemble de \( X \) est ouvert :

• Par définition, \( \emptyset \) et \( \{a, b, c\} \) sont ouverts.
• Les singletons \( \{a\} \), \( \{b\} \), \( \{c\} \) le sont également, chaque point étant ouvert dans cette topologie.
• Les sous-ensembles à deux éléments comme \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \) sont aussi ouverts.

Si l’on considère l’ensemble \( A = \{b, c\} \),

son intérieur est, par définition, l’union de tous les ouverts inclus dans \( A \).

Dans ce cas, ces ouverts sont \( \{b\} \), \( \{c\} \) et \( \{b, c\} \) lui-même.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

On retrouve bien que \( \text{Int}(A) = A \).

Remarque : Ce résultat vaut pour tout sous-ensemble \( S \subseteq X \) dans une topologie discrète. En effet, tous les sous-ensembles y sont ouverts, donc \( \text{Int}(S) = S \).

Théorème de l’intérieur d’un ensemble

Dans un espace topologique \( X \), étant donné un sous-ensemble \( S \) et un point \( y \in X \), on dit que \( y \) appartient à l’intérieur de \( S \), noté \( \operatorname{Int}(S) \), si et seulement s’il existe un ouvert \( U \) tel que \( y \in U \subseteq S \). Formellement : $$ y \in \text{Int}(S) \iff \exists \ U \text{ ouvert, avec } y \in U \subseteq S $$

Autrement dit, un point \( y \) est intérieur à \( S \) s’il existe un voisinage ouvert qui le contient et qui est entièrement inclus dans \( S \).

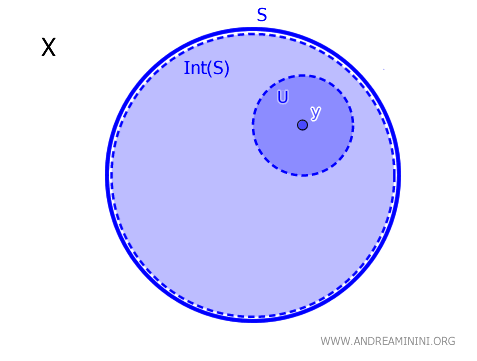
Ce théorème fournit un critère à la fois nécessaire et suffisant pour déterminer si un point \( y \) appartient à l’intérieur d’un ensemble \( S \) dans un espace topologique \( X \).

Démonstration

• Condition nécessaire : Si \( y \in \operatorname{Int}(S) \), alors, par définition, il existe un ouvert \( U \subseteq X \) tel que \( y \in U \subseteq S \). Cette implication découle directement de la définition même de l’intérieur.
• Condition suffisante : Si un ouvert \( U \) existe avec \( y \in U \subseteq S \), alors, par définition, \( y \) appartient à l’intérieur de \( S \), puisque l’intérieur est l’union de tous les ouverts contenus dans \( S \).

Remarque : Ce théorème est fondamental car il établit un lien clair entre la notion d’ouvert et l’appartenance à l’intérieur d’un ensemble. Il joue un rôle central dans l’analyse de la continuité et d’autres concepts topologiques majeurs.

Exemple

Considérons l’ensemble \( A = [1,3] \), soit l’intervalle fermé de 1 à 3 dans \( \mathbb{R} \), muni de la topologie usuelle.

$$ A = [1,3] $$

Cet ensemble contient tous les réels compris entre 1 et 3, bornes incluses.

Pour en déterminer l’intérieur, nous appliquons le théorème énoncé ci-dessus.

Détermination de l’intérieur de \( A \)

Nous cherchons un ouvert \( U \) tel que \( U \subseteq A \) et dont tous les points appartiennent à \( \operatorname{Int}(A) \).

1. Choix de \( U \)
   Prenons \( U = (1,3) \), l’intervalle ouvert excluant les bornes. Cet ensemble est un ouvert de \( \mathbb{R} \) dans la topologie usuelle.
2. Vérification de \( U \subseteq A \)
   Tous les points de \( (1,3) \) sont bien inclus dans \( [1,3] \), tandis que les extrémités \( 1 \) et \( 3 \) n’appartiennent pas à \( U \).

Ainsi, \( U \) est un ouvert contenu dans \( A \), et tous ses points appartiennent à \( \operatorname{Int}(A) \). Par conséquent, l’intérieur de \( A \) est exactement \( (1,3) \).

Remarque : Les extrémités 1 et 3 ne font pas partie de \( \operatorname{Int}(A) \), car il n’existe aucun ouvert contenu dans \( A \) qui les contienne. Cela illustre bien la précision du théorème.

Propriétés de l’intérieur

On présente ici plusieurs propriétés fondamentales de l’intérieur dans un espace topologique. Elles révèlent les interactions profondes entre les opérations topologiques comme l’intérieur, l’adhérence, l’union ou l’intersection. Certaines peuvent paraître contre-intuitives au premier abord.

• Propriété de l’union des intérieurs
  L’union des intérieurs est toujours incluse dans l’intérieur de l’union, mais cette inclusion peut être stricte. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
• Propriété de l’intersection des intérieurs
  L’intérieur de l’intersection de deux ensembles est exactement l’intersection de leurs intérieurs. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• Lien entre l’intérieur du complémentaire et le complémentaire de l’adhérence
  On a l’égalité suivante : $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• Lien entre l’adhérence du complémentaire et le complémentaire de l’intérieur
  De même, on a : $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Remarques

Voici quelques observations complémentaires sur l’intérieur d’un ensemble :

• Si \( U \) est un ouvert de \( X \) et \( U \subseteq A \), alors \( U \subseteq \operatorname{Int}(A) \)
  Tout ouvert inclus dans un ensemble est également contenu dans son intérieur, puisque celui-ci est, par définition, le plus grand ouvert contenu dans l’ensemble.
• Si \( A \subseteq B \), alors \( \operatorname{Int}(A) \subseteq \operatorname{Int}(B) \)
  L’opération d’intérieur est croissante : si un ensemble est inclus dans un autre, il en va de même pour leurs intérieurs.
• Un ensemble \( A \) est ouvert si et seulement si \( A = \operatorname{Int}(A) \)
  C’est une caractérisation classique des ouverts : un ensemble est ouvert s’il est égal à son intérieur, c’est-à-dire si chacun de ses points possède un voisinage ouvert inclus en lui.
• Comment déterminer l’intérieur d’un ensemble avec R
  Le langage R, très utilisé en analyse et en statistique, permet de calculer efficacement l’intérieur d’un ensemble grâce à ses fonctionnalités avancées de visualisation et de traitement topologique.

Et ainsi de suite.