Ensembles Clopen

On qualifie un ensemble de « clopen » lorsqu’il est à la fois ouvert et fermé dans une topologie donnée.

En d’autres termes, un ensemble clopen remplit simultanément les conditions qui définissent un ensemble ouvert et celles qui définissent un ensemble fermé dans la topologie considérée.

Le terme « clopen » provient de la contraction des mots anglais « closed » (fermé) et « open » (ouvert).

Ces ensembles possèdent à la fois les propriétés caractéristiques des ensembles ouverts et celles des ensembles fermés.

Cela se produit précisément lorsqu’un ensemble et son complémentaire sont tous deux ouverts dans la même topologie.

Remarque : Les ensembles clopen sont rares dans l’ensemble des nombres réels, mais apparaissent dans d’autres espaces topologiques. Ils sont particulièrement intéressants, car ils présentent des propriétés spécifiques et jouent un rôle essentiel dans l’analyse de la structure topologique d’un espace.

Un Exemple Concret

Considérons l’ensemble \(X=\{a,b,c,d\}\), muni d’une topologie \(T\).

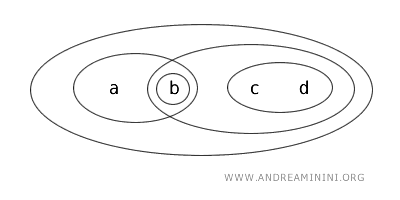
Dans la topologie \(T\), les ensembles définis comme ouverts sont : \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).

Par conséquent, le sous-ensemble \(\{a,b\}\) est un ensemble ouvert dans cette topologie \(T\).

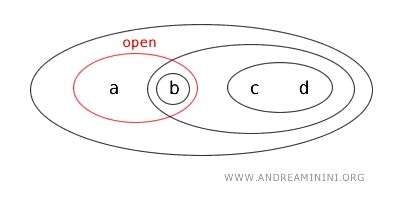
De façon intéressante, l’ensemble \(\{a,b\}\) est également le complémentaire de l’ensemble ouvert \(\{c,d\}\) :

$$ X - \{ c,d \} = \{a , b \} $$

Or, le complémentaire d’un ensemble ouvert est toujours un ensemble fermé :

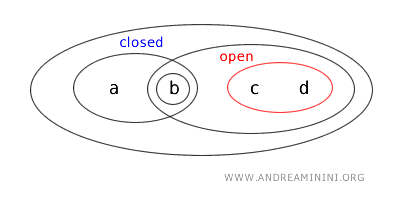
On en conclut donc que l’ensemble \(\{a,b\}\) est également un ensemble fermé.

En définitive, dans la topologie \(T\), l’ensemble \(\{a,b\}\) est à la fois ouvert et fermé, ce qui en fait un ensemble clopen.

L’Ensemble Vide et l’Ensemble Total sont Clopen

Dans toute topologie définie sur un ensemble \(X\), l’ensemble total (\(X\)) et l’ensemble vide (\(\varnothing\)) sont toujours clopen, c’est-à-dire simultanément ouverts et fermés.

Un ensemble est qualifié de clopen s’il satisfait en même temps aux définitions d’ensemble ouvert et d’ensemble fermé dans la topologie considérée.

Rappelons brièvement ces définitions afin de mieux comprendre ce concept.

Selon la définition topologique, l’ensemble vide (\(\varnothing\)) et l’ensemble total (\(X\)) sont toujours considérés comme des ensembles ouverts.

Par ailleurs, d’après la définition d’un ensemble fermé, un ensemble est fermé lorsque son complémentaire est un ensemble ouvert.

À partir de ces définitions, on peut déduire ce qui suit :

• L’ensemble vide (\(\varnothing\))
  Selon les axiomes fondamentaux de la topologie, l’ensemble vide est ouvert. Il est également fermé, puisque son complémentaire \(X \setminus \varnothing = X\) (l’ensemble total) est ouvert. L’ensemble vide est donc à la fois ouvert et fermé, autrement dit clopen.
• L’ensemble total (\(X\))
  L’ensemble total est ouvert par définition. Il est également fermé, puisque son complémentaire \(X \setminus X = \varnothing\) (l’ensemble vide) est ouvert. En conséquence, l’ensemble total est lui aussi clopen.

Ainsi, dans toute topologie, l’ensemble total \(X\) et l’ensemble vide \(\varnothing\) sont toujours des ensembles clopen.

Et ainsi de suite.