Adhérence d’un ensemble

L’adhérence d’un ensemble $ A $ dans un espace topologique $ X $ est l’intersection de tous les ensembles fermés contenant $ A $. Cette intersection est notée $ \text{Cl}(A) $.

L’adhérence de $ A $ est le plus petit ensemble fermé englobant intégralement $ A $.

Il n’existe aucun ensemble fermé contenant $ A $ qui soit strictement plus petit que son adhérence.

Remarque : Cette propriété découle immédiatement de la définition de l’adhérence, puisqu’elle est obtenue comme intersection de tous les ensembles fermés contenant $ A $. Autrement dit, l’adhérence constitue le plus petit ensemble fermé susceptible d’inclure $ A $ : elle est composée de tous les éléments communs à ces ensembles fermés.

Formellement, l’adhérence de $ A $ s’écrit :

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ et } C \text{ est fermé dans } X \} $$

Ici, $ \text{Cl}(A) $ désigne l’adhérence de $ A $, et le symbole $ \bigcap $ représente l’intersection de tous les ensembles fermés $ C $ contenant $ A $.

L’adhérence de $ A $ comprend à la fois les éléments de $ A $ et l’ensemble de ses points d’accumulation dans $ X $.

Remarque : Il convient de souligner que l’adhérence d’un ensemble $ A $ dépend avant tout de la topologie de l’espace $ X $ dans lequel il est défini, bien plus que des propriétés intrinsèques de $ A $. Par conséquent, selon la topologie choisie, l’adhérence de $ A $ peut varier.

Un exemple illustratif
Le théorème de l’adhérence d’un ensemble
Propriétés de l’adhérence dans les espaces topologiques
Observations essentielles

Un exemple illustratif

Considérons l’ensemble $ A = (0, 1) $ dans $ \mathbb{R} $, muni de la topologie usuelle.

Il s’agit de l’intervalle ouvert contenant tous les réels strictement compris entre 0 et 1, à l’exclusion des bornes.

Dans ce cadre, l’adhérence de $ A $ est donnée par $ [0, 1] $.

$$ \text{Cl}(A) = [0,1] $$

Ce nouvel ensemble contient l’intervalle initial $ (0,1) $ ainsi que ses points d’accumulation, à savoir les extrémités 0 et 1.

Remarque : Dans la topologie usuelle sur $ \mathbb{R} $, un ensemble est fermé s’il contient tous ses points d’accumulation. Un point est dit d’accumulation s’il admet, dans tout voisinage, au moins un autre point de l’ensemble. Par exemple, l’intersection des intervalles fermés [0,2] et [-1,1] donne [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Il n’existe aucun intervalle fermé plus petit qui contienne $ (0,1) $.

Exemple 2

Examinons maintenant l’ensemble $ A = [0, 1) $ dans $ \mathbb{R} $, toujours muni de la topologie usuelle.

Il s’agit d’un intervalle fermé à gauche et ouvert à droite, contenant tous les réels de 0 inclus à 1 exclu.

L’adhérence de cet ensemble est, une fois encore, $ [0,1] $.

$$ \text{Cl}(A) = [0,1] $$

En effet, le point 0 appartient déjà à $ A $, tandis que 1 est un point d’accumulation extérieur.

Ainsi, l’adhérence de $ A $ comprend également l’extrémité droite, ce qui donne l’ensemble fermé $ [0,1] $, le plus petit possible contenant $ A $.

Remarque : Ce résultat illustre parfaitement la définition topologique de l’adhérence, qui inclut nécessairement tous les points d’accumulation. Par exemple, l’intersection de [0,2] et [-1,1] est égale à [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$

Exemple 3

Considérons maintenant le même ensemble $ A = [0,1) $, mais cette fois dans un espace $ X $ muni de la topologie discrète.

Dans cette topologie, tout sous-ensemble est simultanément ouvert et fermé.

Ensemble ouvert
Dans un espace muni de la topologie discrète, tout sous-ensemble de $ X $ est un ouvert. Ainsi, $ A \subset X $ implique que $ A $ est ouvert.
Ensemble fermé
De même, chaque sous-ensemble de $ X $ est aussi fermé, puisque son complément est un ouvert. Par exemple, $ X/A $, étant un sous-ensemble de $ X $, est ouvert, donc $ A $ est également fermé.

Autrement dit, tout ensemble est cloche (ou *clopen*), c’est-à-dire à la fois ouvert et fermé.

Par conséquent, l’adhérence de $ A $ coïncide exactement avec $ A $ lui-même, puisqu’il est déjà fermé.

$$ \text{Cl}(A) = [0,1) $$

L’ensemble fermé minimal contenant $ A $ n’est autre que $ A $ lui-même.

Remarque : Cet exemple montre clairement à quel point la structure topologique de l’espace peut modifier l’adhérence d’un ensemble. Comme nous l’avons souligné, le fait qu’un ensemble soit fermé dépend de la topologie de $ X $, et non de la nature de l’ensemble lui-même.

Exemple 4

Considérons un espace topologique $ X $ formé des points $ \{a, b, c\} $, muni de la topologie discrète.

Dans ce contexte, tout sous-ensemble de $ X $ est un ouvert :

Les ensembles $ \emptyset $ et $ \{a, b, c\} $ sont ouverts par définition.
Les singletons $ \{a\} $, $ \{b\} $, $ \{c\} $ le sont également.
Et toute combinaison de ces éléments, comme $ \{a, b\} $, $ \{a, c\} $, $ \{b, c\} $, est aussi un ouvert.

De plus, comme le complémentaire de tout sous-ensemble est aussi un élément de $ X $ et donc un ouvert, tous les sous-ensembles sont à la fois ouverts et fermés.

Si l’on prend l’ensemble $ A = \{b, c\} $, on observe qu’il est ouvert comme tout sous-ensemble de $ X $, et aussi fermé puisque son complément $ X/A = \{a\} $ est ouvert.

L’adhérence de $ A $, notée $ \text{Cl}(A) $, correspond à l’intersection de tous les ensembles fermés contenant $ A $. Dans ce cas, aucun ajout n’est nécessaire.

On a donc simplement :

\[ \text{Cl}(A) = \{b, c\} \]

Dans une topologie discrète, chaque ensemble est déjà fermé, de sorte que l’adhérence coïncide toujours avec l’ensemble d’origine.

Remarque : Pour s’en convaincre, on peut constater que les ensembles fermés contenant $ A $ sont $ \{b, c\} $ et $ \{a, b, c\} $. $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\} $$ L’intersection donne exactement $ A $, donc $ \text{Cl}(A) = A $.

Le théorème de l’adhérence d’un ensemble

Dans un espace topologique $ X $, un point $ y $ appartient à l’adhérence d’un sous-ensemble $ S $, notée $ \text{Cl}(S) $, si et seulement si tout ouvert $ U $ contenant $ y $ rencontre $ S $ : $ y \in \text{Cl}(S) \iff \forall \ U \text{ ouvert tel que } y \in U, \ U \cap S \neq \emptyset $.

Autrement dit, pour qu’un point $ y \in X $ appartienne à l’adhérence de $ S $, il faut que chaque voisinage ouvert de $ y $ contienne au moins un élément de $ S $.

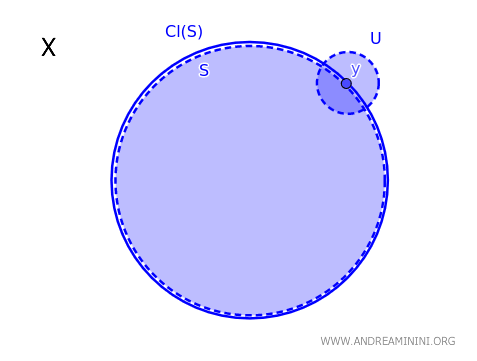
visual example

Ce théorème fournit un critère fondamental pour caractériser l’appartenance d’un point à l’adhérence d’un ensemble $ S $ dans un espace topologique $ X $.

Démonstration

Condition nécessaire : Si $ y \in \text{Cl}(S) $, alors, par définition, tout ouvert contenant $ y $ doit intersecter $ S $. Cela s’explique par le fait que l’adhérence d’un ensemble comprend à la fois ses points intérieurs et ses points d’accumulation. Un point d’accumulation est un point dont tout voisinage contient au moins un point de $ S $, distinct ou non de lui-même.
Condition suffisante : Réciproquement, si tout ouvert contenant $ y $ rencontre $ S $, alors $ y $ est nécessairement soit un point de $ S $, soit un point d’accumulation de $ S $. Dans les deux cas, $ y $ appartient à $ \text{Cl}(S) $, puisqu’aucun ouvert le contenant n’est disjoint de $ S $.

Remarque : Ce théorème constitue un résultat central de la topologie générale. Il établit un lien clair entre la notion d’ouvert et la structure de l’adhérence. Il intervient dans des domaines variés tels que la continuité des fonctions, la convergence des suites et des réseaux, ainsi que dans de nombreuses démonstrations fondamentales.

Exemple

Considérons l’ensemble $ A = (0, 2) $, muni de la topologie usuelle sur $ \mathbb{R} $, c’est-à-dire un intervalle ouvert de l’ensemble des réels.

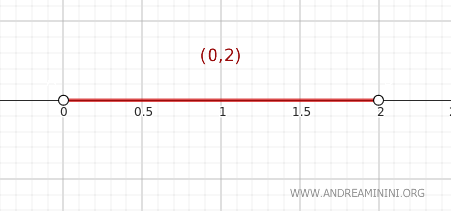
example

Appliquons le théorème pour déterminer si un point $ y $ appartient à $ \text{Cl}(A) $.

Choisissons par exemple le point $ y = 2 \in \mathbb{R} $.

D’après le théorème, $ y \in \text{Cl}(A) $ si et seulement si tout ouvert contenant $ y $ coupe $ A $.

Analyse des voisinages de $ y $ : Tout intervalle ouvert contenant $ y = 2 $, tel que $ (1{,}9, 2{,}1) $, $ (1{,}95, 2{,}05) $ ou $ (1{,}99, 2{,}01) $, contient nécessairement des points de $ A = (0, 2) $, comme $ 1{,}95 $ ou $ 1{,}99 $, qui y appartiennent clairement.
Vérification de l’intersection : Puisque tout voisinage ouvert de $ y = 2 $ contient des points de $ A $, il s’ensuit, conformément au théorème, que $ y = 2 $ appartient bien à $ \text{Cl}(A) $.

Ainsi, le point $ y = 2 $ appartient à l’adhérence de $ A $, car aucun de ses voisinages n’est entièrement disjoint de $ A $.

$$ y \in \text{Cl}(A) $$

On en déduit que l’adhérence de $ A $ est l’intervalle fermé $ \text{Cl}(A) = [0, 2] $, qui contient explicitement le point $ y = 2 $.

Propriétés de l’adhérence dans les espaces topologiques

Cette section présente plusieurs propriétés fondamentales de l’adhérence dans un espace topologique, ainsi que certaines relations subtiles avec l’intérieur, souvent contre-intuitives au premier abord.

Intérieur du complément et complément de l’adhérence
L’intérieur du complément d’un ensemble $ A $ est égal au complément de son adhérence. Cette relation s’écrit : $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
Adhérence du complément et complément de l’intérieur
L’adhérence du complément d’un ensemble $ A $ coïncide avec le complément de son intérieur : $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

Observations essentielles

Voici quelques propriétés clés de l’adhérence, accompagnées d’une brève justification conceptuelle :

Si $ C $ est fermé dans $ X $ et $ A \subseteq C $, alors $ \text{Cl}(A) \subseteq C $
Si $ A $ est inclus dans un ensemble fermé $ C $, alors son adhérence l’est aussi. En effet, $ \text{Cl}(A) $ étant le plus petit fermé contenant $ A $, il est nécessairement inclus dans tout fermé qui le contient.
Si $ A \subseteq B $, alors $ \text{Cl}(A) \subseteq \text{Cl}(B) $
L’adhérence est une opération monotone : si $ A \subseteq B $, alors tout point adhérent à $ A $ l’est aussi à $ B $, donc $ \text{Cl}(A) \subseteq \text{Cl}(B) $.
Un ensemble $ A $ est fermé si et seulement si $ A = \text{Cl}(A) $
Un ensemble est fermé précisément lorsqu’il contient tous ses points d’adhérence, c’est-à-dire lorsqu’il coïncide avec sa propre adhérence. C’est là une caractérisation fondamentale des fermés en topologie.
L’adhérence d’un ensemble est l’union de celui-ci avec ses points d’accumulation
Soit $ A $ un ensemble et $ A' $ l’ensemble de ses points d’accumulation, alors : $$ \text{Cl}(A) = A \cup A' $$
Idempotence
L’adhérence est idempotente : l’appliquer plusieurs fois ne change rien au résultat : $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
Inclusion de l’ensemble initial
Tout ensemble est contenu dans sa propre adhérence : $$ A \subseteq \text{Cl}(A) $$

D’autres contenus seront proposés prochainement.