Convergence dans un espace topologique

Dans un espace topologique $ X $, on dit qu’un point $ x \in X $ est la limite d’une suite $ (x_n) $ si, pour tout voisinage $ U $ de $ x $, il existe un entier positif $ N $ tel que, pour tout $ n \geq N $, on ait $ x_n \in U $.

Autrement dit, la suite $ (x_n) $ converge vers $ x $ si, à partir d’un certain rang, tous ses termes restent contenus dans n’importe quel voisinage de $ x $.

Cette définition s’écrit formellement :

$$ \lim_{n \to \infty} x_n = x $$

Dans ce cas, on dit que $ x $ est la limite de la suite $ (x_n) $.

Exemple illustratif

Étudions un exemple concret avec la suite $ \left( \frac{1}{n} \right) $ dans l’espace topologique $ X = \mathbb{R} $, muni de la topologie usuelle.

$$ x_n = \left( \frac{1}{n} \right) $$

Nous voulons démontrer que $ \left( \frac{1}{n} \right) $ converge vers 0, c’est-à-dire que $ 0 $ est la limite de cette suite.

Considérons un voisinage arbitraire $ U $ de $ 0 $.

Dans la topologie usuelle sur $ \mathbb{R} $, tout voisinage de $ 0 $ contient un intervalle ouvert de la forme $ (-\epsilon, \epsilon) $, avec $ \epsilon > 0 $.

Nous devons trouver un entier $ N \in \mathbb{N} $ tel que, pour tout $ n \geq N $, on ait $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Étant donné $ \epsilon > 0 $, il suffit de choisir $$ N = \left\lceil \frac{1}{\epsilon} \right\rceil. $$ Alors, pour tout $ n \geq N $, on a :

$$ n \geq \frac{1}{\epsilon} \quad \Rightarrow \quad \frac{1}{n} \leq \epsilon $$

Ce qui implique : $$ \left| \frac{1}{n} \right| < \epsilon \quad \text{pour tout } n \geq N. $$

Ainsi, pour tout voisinage $ U $ de $ 0 $, il existe un rang $ N $ tel que tous les termes ultérieurs de la suite se trouvent dans $ U $. En conséquence, $$ \lim_{n \to \infty} \frac{1}{n} = 0 $$

Cela montre que $ 0 $ est bien la limite de la suite $ \left( \frac{1}{n} \right) $.

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

En d’autres termes, la suite $ \frac{1}{n} $ converge vers zéro car, à partir d’un certain rang, tous ses termes demeurent dans n’importe quel voisinage de zéro.

Voici, à titre d’illustration, un tableau indiquant les dix premiers termes de la suite :

$$ \begin{array}{|c|c|} \hline n & \frac{1}{n} \\ \hline 1 & 1 \\ 2 & 0.5 \\ 3 & 0.333 \\ 4 & 0.25 \\ 5 & 0.2 \\ 6 & 0.167 \\ 7 & 0.143 \\ 8 & 0.125 \\ 9 & 0.111 \\ 10 & 0.1 \\ \hline \end{array} $$

Par exemple, si l’on choisit $ N = 5 $, de sorte que $ x_5 = \frac{1}{5} = 0.2 $, alors pour tout $ n > 5 $, les termes suivants de la suite appartiennent au voisinage $ U = (0, 0.2) $.

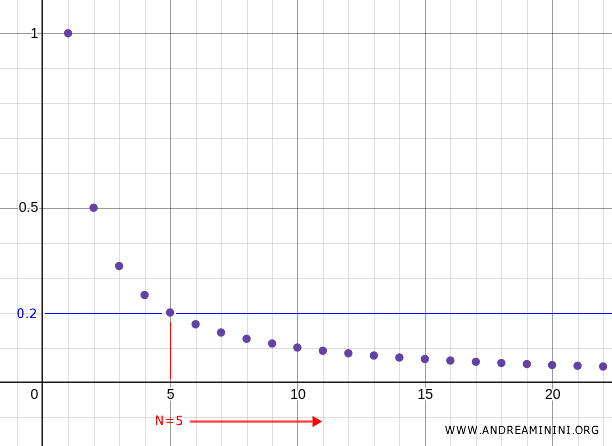
ejemplo de punto de convergencia

Il en va de même quel que soit le choix de $ N $.

Par exemple, si l’on prend $ N = 10 $, alors $ x_{10} = 0.1 $, et pour tout $ n > 10 $, les termes de la suite se trouvent dans le voisinage $ U = (0, 0.1) $, et ainsi de suite.

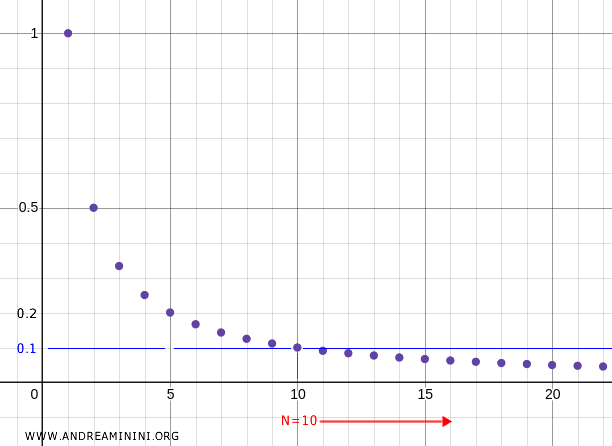
visualización de la sucesión convergente

Nous concluons donc que $ 0 $ est bien la limite de la suite.

Et ainsi de suite.