La Topologie Usuelle d'un Ensemble Ouvert

La topologie usuelle (ou standard) sur $ \mathbb{R} $ est définie à partir des intervalles ouverts $ (a, b) $, avec $ a < b $, ainsi que de toute réunion, finie ou infinie, de tels intervalles, lesquels sont considérés comme des ensembles ouverts.

Plus formellement, un ensemble $ U $ est dit ouvert si, pour tout point $ x \in U $, il existe un intervalle ouvert $ (a, b) $ tel que $ x \in (a, b) $ et $ (a, b) \subseteq U $.

$$ x \in (a,b) \subseteq U $$

Autrement dit, chaque point $ x $ d’un ensemble ouvert $ U $ est contenu dans un intervalle ouvert entièrement inclus dans $ U $.

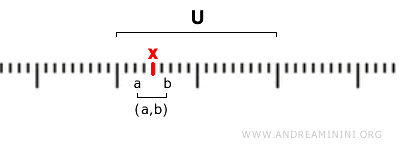
ejemplo de un conjunto abierto

Dans la topologie usuelle, on considère comme ouverts les ensembles suivants :

Intervalles ouverts
Les ensembles ouverts de la topologie usuelle sur $ \mathbb{R} $ sont précisément les intervalles ouverts $ (a, b) $ avec $ a < b $, ainsi que toute réunion, finie ou infinie, de tels intervalles.
Opérations sur les ensembles ouverts
Dans ce cadre topologique, les opérations d’union et d’intersection finie préservent l’ouverture.
- Unions : Toute union, même infinie, d’ensembles ouverts reste un ensemble ouvert.
- Intersections finies : L’intersection d’un nombre fini d’ensembles ouverts est également un ensemble ouvert.

La topologie usuelle n’est qu’un exemple parmi de nombreuses topologies possibles sur un ensemble $ X $. On la qualifie de « usuelle » ou « standard » car elle est la plus utilisée et joue un rôle fondamental dans de nombreux domaines des mathématiques.

Elle est privilégiée car elle reflète de façon naturelle des notions intuitives comme la proximité, l’ouverture et la continuité, en particulier sur la droite réelle $ \mathbb{R} $.

Remarque : Sur $ \mathbb{R} $ et d'autres espaces, il existe des topologies alternatives fondées sur des bases différentes, qui donnent lieu à des ensembles ouverts obéissant à d'autres règles. Ces variantes sont souvent conçues pour étudier des propriétés spécifiques ou pour aborder les structures mathématiques sous un autre angle.

Exemple Pratique

La base de la topologie usuelle sur $ \mathbb{R} $ est constituée de tous les intervalles ouverts $ (a, b) $, avec $ a < b $.

$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$

Une propriété essentielle de cette topologie est que, pour tout point $ x $ appartenant à un ensemble ouvert $ U $, on peut toujours trouver un intervalle ouvert centré en $ x $, entièrement contenu dans $ U $, ce qui satisfait à la définition d’un ensemble ouvert dans la topologie usuelle.

$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$

Autrement dit, $ U $ est un ensemble ouvert dans la topologie usuelle sur $ \mathbb{R} $.

On parle de topologie « usuelle » car c’est celle que l’on utilise le plus fréquemment sur la droite réelle, notamment pour formaliser rigoureusement les notions de continuité et de limite.

Exemple 2

Considérons l’intervalle $ (0,1) $, qui exclut les bornes $ 0 $ et $ 1 $, et analysons sa structure topologique selon la topologie usuelle.

Nous cherchons à savoir si cet ensemble peut être considéré comme un espace topologique.

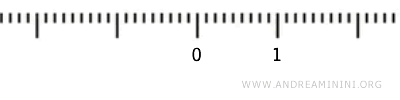
el caso del intervalo (0,1)

Dans le cadre de la topologie induite, un sous-ensemble $ U \subset (0, 1) $ est ouvert dans $ (0,1) $ si, pour chaque point $ x \in U $, il existe un intervalle ouvert $ (a, b) $ de $ \mathbb{R} $ tel que $ x \in (a, b) $ et $ (a, b) \cap (0,1) \subseteq U $.

On remarque que l’intervalle $ (0,1) $ peut être exprimé comme l’intersection de plusieurs ensembles ouverts dans la topologie usuelle de $ \mathbb{R} $, ce qui garantit qu’il hérite d’une structure topologique bien définie.

Ainsi, l’intervalle $ (0,1) $ forme un espace topologique muni de la topologie induite par la topologie standard de $ \mathbb{R} $.

Par exemple, les intervalles $ (0.1, 0.5) $, $ (0.2, 0.9) $, ou encore leur réunion comme $ (0.1, 0.5) \cup (0.6, 0.8) $, sont des ensembles ouverts de $ (0,1) $ dans la topologie induite. Autrement dit, les ouverts de $ (0,1) $ sont exactement les ensembles ouverts de $ \mathbb{R} $ dont l’intersection avec $ (0,1) $ reste entièrement contenue dans cet intervalle.

Comme $ (0,1) $ est un sous-espace topologique de $ \mathbb{R} $, il en hérite toutes les propriétés fondamentales.

Exemple 3

Considérons l’ensemble fini $ X = \{1,2,3\} $, formé de trois entiers naturels.

On souhaite déterminer si l’on peut munir $ X $ d’une structure topologique issue de la topologie standard sur $ \mathbb{R} $.

Ici, les éléments isolés de $ X $ ne peuvent pas être considérés comme ouverts, car la base de la topologie standard est formée d’intervalles ouverts, ce qui ne correspond pas naturellement à un ensemble discret comme $ X $.

Par exemple, si l’on considère l’élément $ \{2\} $ de $ X $, on peut bien le placer dans un intervalle ouvert $ (2-\epsilon, 2+\epsilon) $, mais cet intervalle contient une infinité de réels qui ne font pas partie de $ X $. Ainsi, $ \{2\} $ ne peut pas être considéré comme un ensemble ouvert dans la topologie standard sur $ \mathbb{R} $.
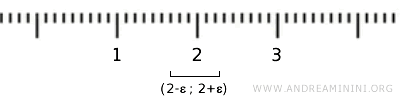
ejemplo con el número 2

Si l’on considère $ X $ comme un sous-ensemble de $ \mathbb{R} $, la « topologie induite » ou « topologie de sous-espace » sur $ X $ ne contient que deux ouverts : l’ensemble vide et l’ensemble $ X $ lui-même, ce qui reste trivial d’un point de vue topologique.

Pour doter un ensemble fini comme $ X $ d’une structure topologique plus riche, on utilise généralement la topologie discrète, dans laquelle tous les sous-ensembles de $ X $ sont considérés comme ouverts par définition.

Et ainsi de suite.