Ensembles ouverts en topologie
Un ensemble A est dit ouvert si, pour tout élément x appartenant à l'ensemble (x∈A), il existe un voisinage qui appartient également à l'ensemble.
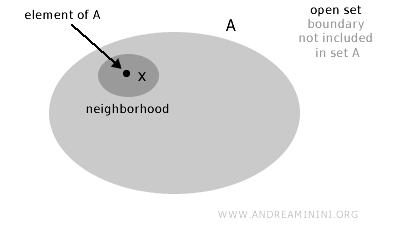
Autrement dit, un ensemble est considéré comme ouvert si, intuitivement, ses « frontières » ne font pas partie de l'ensemble lui-même.
Plus formellement, un ensemble A dans un espace topologique X est ouvert si, pour tout point x dans A, il existe un voisinage de x qui est entièrement contenu dans A.
Note. Cela signifie que autour de chaque point de l'ensemble, vous pouvez trouver une « région » qui est totalement englobée par l'ensemble, sans « toucher » la limite extérieure de l'ensemble.
Un exemple pratique
Un exemple simple d'un ensemble ouvert sur une ligne est un intervalle ouvert.
Qu'est-ce qu'un intervalle ouvert ? Un intervalle ouvert de R est l'ensemble des réels x tels que a < x < b, où a et b sont deux nombres réels vérifiant a < b.
Cet intervalle est noté (a,b), où les parenthèses rondes indiquent que les points extrêmes a et b ne sont pas inclus dans l'ensemble.
Par exemple, l'intervalle ouvert (3,10) est un ensemble ouvert sur la ligne réelle.
Dans ce cas, l'ensemble A comprend une infinité de nombres entre 3 et 10, exclus.
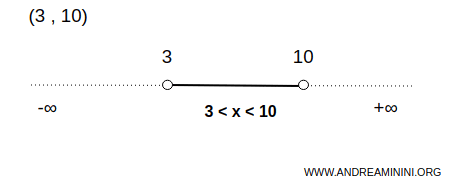
Cela signifie que pour chaque point x à l'intérieur de cet intervalle, il existe toujours un petit intervalle ouvert autour de x qui est complètement contenu dans (3,10).
Par exemple, pour le point x=3.1, je peux prendre l'intervalle ouvert (3.09,3.11) qui est entièrement contenu dans (3,10).
Il en va de même pour tout autre élément à l'intérieur de l'intervalle (3,10), car entre deux nombres réels, il existe une infinité de nombres réels.
Note. Même si je considère un très petit nombre réel à l'intérieur de l'intervalle (3,10), par exemple 3.001, je peux encore construire un voisinage 3.001±0.00000001 qui inclut une infinité de nombres réels à l'intérieur de l'intervalle ouvert (3,10).
C'est un exemple simple en une dimension d'un ensemble ouvert.
Autres exemples
Le même concept peut être étendu à un espace bidimensionnel, comme le plan.
Par exemple, l'ensemble des points d'un cercle de rayon r=1 et de centre à l'origine (0;0).
$$ x^2+y^2<1 $$
Cette inégalité décrit l'ensemble de tous les points dont la distance par rapport au centre (0,0) est inférieure à 1, donc SANS inclure les points sur la circonférence mais seulement ceux à l'intérieur du cercle.
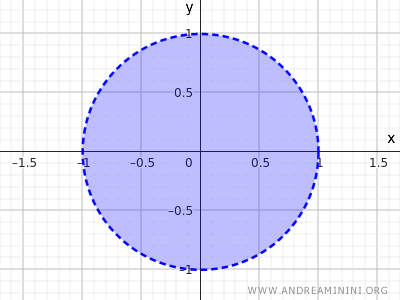
C'est un autre exemple d'ensemble ouvert.
Quand un ensemble est-il fermé ?
Pour avoir un ensemble fermé, il suffit d'inclure les points sur la circonférence dans l'ensemble.
$$ x^2+y^2 \le 1 $$
Dans ce cas, la condition selon laquelle chaque élément de l'ensemble possède un voisinage contenu dans l'ensemble ne s'applique plus.
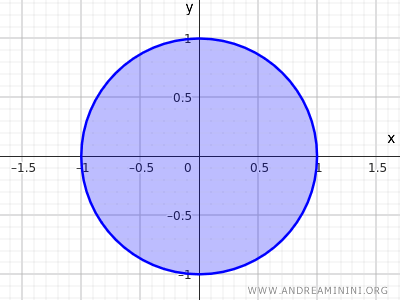
Dans le cas d'un ensemble fermé, les points sur la circonférence n'ont pas de voisinage entièrement contenu dans l'ensemble.
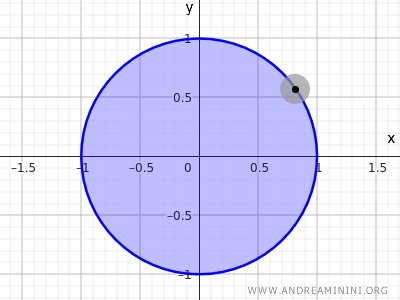
Note. En topologie, l'équation définissant un cercle $ x^2 +y^2=1 $ n'est ni un ensemble ouvert ni un ensemble fermé dans l'espace euclidien R2 parce qu'elle ne considère que les points sur la circonférence, sans les points à l'intérieur. En revanche, l'ensemble des points défini par l'inégalité $ x^2+y^2<1 $, qui inclut les points internes mais pas ceux de la circonférence, est un exemple d'ensemble ouvert. Y compris aussi les points de la circonférence $ x^2+y^2\le 1 $ résulterait dans un ensemble fermé.
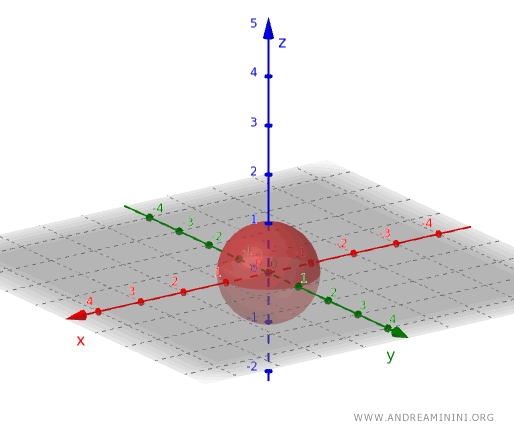
En appliquant le même principe, un ensemble ouvert dans un espace tridimensionnel peut être créé en considérant, par exemple, l'ensemble des points situés à l'intérieur d'une sphère, en excluant cependant ceux qui se trouvent sur sa surface.
Choisir une topologie
Les intervalles ouverts sont très utiles car ils sont intuitifs et donnent immédiatement une idée de ce qu'est un ensemble ouvert.
Cependant, le concept d'ensemble ouvert est bien plus abstrait et ne devrait pas être limité à de simples intervalles ouverts.
Par conséquent, une fois le concept compris, il convient de l'approfondir.
Le concept d'« ensemble ouvert » dépend de la topologie choisie pour s'appliquer à un espace.
L'idée clé à saisir est que la définition des ensembles ouverts peut varier considérablement en fonction de la topologie appliquée à un espace.
Dans certains espaces, un ensemble qui semble « fermé » dans une topologie standard peut être considéré comme « ouvert » dans une autre topologie.
En d'autres termes, tout ensemble peut être considéré comme ouvert en fonction de la topologie définie pour un espace.
Qu'est-ce qu'une topologie ? Une topologie sur un espace est essentiellement une collection d'ensembles considérés comme « ouverts » selon certaines règles que ces ensembles doivent respecter, telles que l'union arbitraire d'ensembles ouverts restant un ensemble ouvert et l'intersection d'un nombre fini d'ensembles ouverts restant un ensemble ouvert.
Pour cette raison, il est conseillé de ne pas limiter sa réflexion aux exemples les plus courants et intuitifs d'ensembles ouverts, tels que les intervalles ouverts ou les disques ouverts.
En topologie, la définition d'« ensemble ouvert » est bien plus large et peut inclure des ensembles qui, à première vue, pourraient ne pas sembler l'être.
Un exemple pratique
Considérons l'espace \( \{a, b\} \) ne contenant que deux éléments.
Dans cet espace, au moins deux topologies différentes peuvent être définies : la topologie triviale et la topologie discrète.
- Topologie Triviale
Dans la topologie triviale sur \( \{a, b\} \), les seuls ensembles ouverts sont l'ensemble vide \( \emptyset \) et l'espace lui-même \( \{a, b\} \). C'est la topologie la plus simple possible, avec pratiquement aucune « structure ouverte » au-delà de l'espace total et de l'ensemble vide. - Topologie Discrète
Dans la topologie discrète, chaque sous-ensemble possible de \( \{a, b\} \) est considéré comme ouvert. Cela signifie que \( \{a\} \), \( \{b\} \), \( \{a, b\} \), et \( \emptyset \) sont tous ouverts. La topologie discrète est la plus « riche » en termes d'ensembles ouverts, car chaque combinaison de points forme un ensemble ouvert.
Maintenant, considérons l'ensemble \( \{a\} \) dans les deux topologies :
- Dans la topologie triviale, l'ensemble {a} n'est pas ouvert
Le seul ensemble ouvert contenant des éléments est \( \{a, b\} \), outre l'ensemble vide. - Dans la topologie discrète, l'ensemble {a} est ouvert
Dans cette topologie, chaque sous-ensemble de \( \{a, b\} \), y compris \( \{a\} \) et \( \{b\} \), sont des ensembles ouverts par définition.
Ainsi, l'ensemble \( \{a\} \) est un ensemble ouvert selon la topologie discrète, mais pas selon la topologie triviale.
Cet exemple simple met en évidence comment la définition d'un ensemble ouvert est étroitement liée à la topologie choisie.
Théorème sur les ensembles ouverts
Théorème 1
Étant donné un ensemble ouvert X et une topologie T qui forment ensemble un espace topologique (X,T), un sous-ensemble S⊂X est un ensemble ouvert dans l'espace topologique (X,T) si chaque élément (ou point) s∈S possède un voisinage U qui est entièrement contenu dans le sous-ensemble S, signifiant U⊂S.
Par définition, S est un ensemble ouvert parce qu'il fait partie de l'espace topologique (X,T).
Ainsi, le sous-ensemble S peut être vu comme le voisinage de chacun de ses éléments (points) s∈S.
De cela, je déduis que le voisinage Us de chaque élément s∈S est, à son tour, un ensemble ouvert contenu dans S.
$$ x \in U_s ⊂ S ⊂ X $$
Un ensemble ouvert peut être vu comme l'union des voisinages ouverts de ses points.
Ainsi, si j'observe que chaque élément (point) s∈S d'un sous-ensemble S a un voisinage Us⊂S contenu dans S, je peux conclure que l'ensemble S est un ensemble ouvert car il est l'union d'ensembles ouverts.
En d'autres termes, un ensemble est ouvert si et seulement si, pour chaque point à l'intérieur de l'ensemble, il existe un voisinage de ce point qui est complètement contenu dans l'ensemble.
Exemple. Imaginez une table parsemée de billes de verre. Chaque bille représente un point à l'intérieur d'un certain ensemble. Dire que cet ensemble est « ouvert » revient à dire qu'il y a assez d'espace autour de chaque bille pour se déplacer librement sans franchir le bord de la table. Si pour chaque bille sur cette table, je peux dessiner un cercle autour d'elle, entièrement contenu sur la table (sans toucher les bords), alors l'ensemble des billes sur la table représente un « ensemble ouvert ». Fondamentalement, l'ouverture de l'ensemble signifie que, peu importe quelle bille je choisis, il y a toujours un peu d'espace « libre » autour d'elle qui appartient encore à l'ensemble des billes sur la table.

Théorème 2
Prenez un ensemble \( X \) et une base \( B \) pour une topologie sur \( X \). Un sous-ensemble \( A \subset X \) se qualifie comme un ensemble ouvert dans la topologie générée par \( B \) si et seulement si, pour chaque élément \( x \) dans \( A \), il existe un élément de base \( B_x \) tel que \( x \) soit à l'intérieur de \( B_x \) et que \( B_x \) soit complètement contenu dans \( A \), signifiant \( B_x \subseteq A \).
Ce théorème met en évidence une caractéristique clé des topologies formées par une base.
En d'autres termes, chaque point dans un ensemble ouvert \( A \) doit avoir un « voisinage » autour de lui, \( B_x \), qui appartient aux ensembles de base et est entièrement englobé par \( A \).
Cela confirme que l'ensemble \( A \) est effectivement ouvert dans la topologie créée par \( B \).
Preuve. Si A est un ensemble ouvert dans la topologie générée par la base B sur l'ensemble X, où A est un sous-ensemble de X, alors par définition, A est l'union des éléments de base. Par conséquent, chaque élément x dans A appartient à au moins un élément de base Bx, et ce Bx est entièrement contenu dans l'ensemble A, signifiant Bx est un sous-ensemble de A, car A est l'union des éléments de base. Ce raisonnement peut être inversé. Si chaque élément x dans A est contenu dans au moins un élément de base Bx qui est entièrement contenu dans A, ou en d'autres termes, Bx est un sous-ensemble de A, alors l'ensemble A est ouvert dans la topologie générée par B.
Exemple
En considérant l'ensemble \( X = \{1, 2, 3, 4, 5\} \) et une base pour une topologie sur \( X \) comme \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \), déterminons si l'ensemble \( A = \{1, 2, 3\} \) est ouvert.
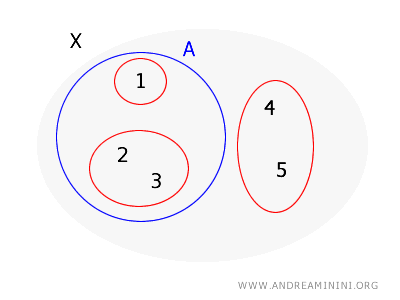
Pour chaque point dans \( A \), je dois trouver un ensemble de base qui le contient et qui est entièrement à l'intérieur de \( A \) :
- Pour le point \( 1 \) dans \( A \), il y a l'ensemble de base \( \{1\} \) qui contient \( 1 \) et est entièrement contenu dans \( A \).
- Pour le point \( 2 \) dans \( A \), l'ensemble de base \( \{2, 3\} \) contient \( 2 \) et est entièrement contenu dans \( A \).
- Pour le point \( 3 \) dans \( A \), le même ensemble de base \( \{2, 3\} \) contient \( 3 \) et est entièrement à l'intérieur de \( A \).
Chaque point dans \( A \) est inclus dans un ensemble de base qui est, à son tour, contenu dans \( A \), remplissant ainsi la condition du théorème.
Ainsi, je peux conclure que \( A \) est un ensemble ouvert dans la topologie générée par la base \( B \).
Exemple 2
En considérant le même ensemble \( X = \{1, 2, 3, 4, 5\} \) et la base pour une topologie sur \( X \) définie comme \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) de l'exemple précédent.
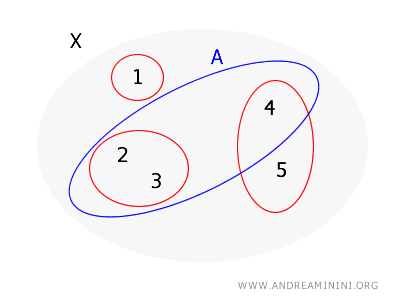
Cette fois, cependant, je veux vérifier si l'ensemble \( A = \{2, 3, 4\} \) est ouvert.
- Pour le point \( 2 \), je peux utiliser l'ensemble de base \( \{2, 3\} \), qui est entièrement à l'intérieur de \( A \).
- Pour le point \( 3 \), il y a le même ensemble de base \( \{2, 3\} \) qui le couvre et est entièrement à l'intérieur de \( A \).
- Pour le point \( 4 \), il n'y a pas d'ensemble de base qui le contienne et qui soit également complètement à l'intérieur de \( A \) parce que le seul ensemble de base qui inclut 4 est \( \{4, 5\} \), qui n'est pas entièrement à l'intérieur de \( A \) (puisqu'il inclut 5, qui n'est pas dans \( A \)).
Par conséquent, selon le théorème, l'ensemble \( A \) n'est pas un ensemble ouvert dans la topologie générée par la base \( B \), car chaque point dans \( A \) n'a pas d'ensemble de base qui est complètement contenu à l'intérieur de \( A \).
Et ainsi de suite.