Topologie métrique
La topologie métrique sur un espace \( X \) est engendrée par une base constituée des boules ouvertes définies à l’aide d’une distance \( d \) sur \( X \). On l'appelle également la topologie induite par la métrique \( d \).
Dans un espace métrique \( (X, d) \), où \( d \) mesure la distance entre les points de \( X \), on définit une topologie formée d’ensembles ouverts construits à partir des "boules ouvertes".
Une "boule ouverte" centrée en un point \( x \in X \), de rayon \( \varepsilon > 0 \), est l’ensemble des points \( y \in X \) tels que la distance à \( x \) soit strictement inférieure à \( \varepsilon \) :
$$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$
Dans une topologie métrique, un ensemble est dit ouvert s’il peut s’écrire comme une union - possiblement infinie - de boules ouvertes.
Autrement dit, un ensemble \( U \subset X \) est ouvert dans la topologie induite par \( d \) si, pour tout point \( y \in U \), il existe un rayon \( \delta > 0 \) tel que la boule \( B_d(y, \delta) \) soit entièrement contenue dans \( U \).
Un exemple concret
Considérons la droite réelle \(\mathbb{R}\), vue comme un espace euclidien unidimensionnel, muni de la distance euclidienne usuelle.
L’ensemble \(\mathbb{R}\) contient tous les nombres réels.
La distance \(d\) entre deux points \(x\) et \(y\) est donnée par :
$$ d(x, y) = |x - y| $$
où \(|x - y|\) désigne la valeur absolue de la différence entre \(x\) et \(y\).
Cette fonction satisfait toutes les propriétés requises pour définir une métrique.
Avec cette distance, on peut construire des boules ouvertes dans \(\mathbb{R}\).
Par exemple, prenons le point \(x = 3\) et un rayon \(\varepsilon = 1\).
La boule ouverte centrée en \(x = 3\) et de rayon \(1\) est :
$$ B_d(3, 1) = \{y \in \mathbb{R} \mid d(3, y) < 1\} = \{y \in \mathbb{R} \mid |3 - y| < 1\} $$
En résolvant l’inégalité \( |3 - y| < 1 \), on trouve que \(2 < y < 4\). Ainsi :
$$ B_d(3, 1) = (2, 4) $$
Autrement dit, la boule ouverte centrée en \(3\) de rayon \(1\) correspond à l’intervalle ouvert \((2, 4)\) sur la droite réelle.
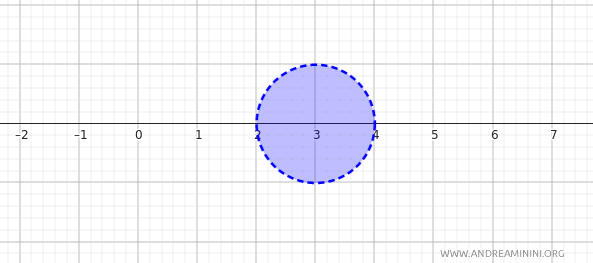
Des ensembles comme \( (2, 4) \), \( (5, 7) \), ou plus généralement tout intervalle ouvert \((a, b)\) de \(\mathbb{R}\), peuvent être interprétés comme des boules ouvertes ou des unions de boules ouvertes associées à la métrique \(d(x, y) = |x - y|\).
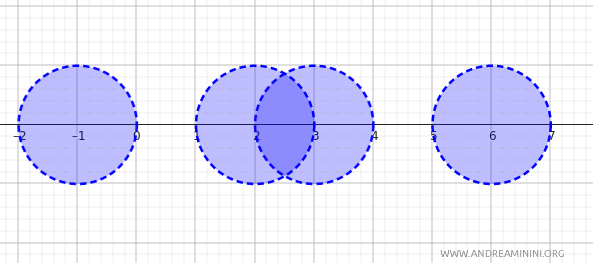
Ces intervalles forment une base pour la topologie métrique sur \(\mathbb{R}\).
Remarque. Dans la topologie métrique de \(\mathbb{R}\), un ensemble est ouvert si, pour chaque point qu’il contient, on peut trouver un intervalle ouvert (c’est-à-dire une boule ouverte) entièrement inclus dans l’ensemble. Par exemple, \((0, 5)\) est un ouvert car, autour de tout point de \((0, 5)\), on peut tracer un petit intervalle qui reste entièrement à l’intérieur de l’ensemble.
En résumé, la métrique \(d(x, y) = |x - y|\) sur \(\mathbb{R}\) engendre la topologie usuelle des intervalles ouverts, appelée aussi topologie métrique de \(\mathbb{R}\).
Ensembles ouverts dans une topologie métrique
Dans une topologie métrique, un sous-ensemble \( U \subset X \) est dit ouvert si, pour tout point \( y \in U \), il existe une boule ouverte centrée en \( y \) - autrement dit, un "voisinage" de rayon \(\delta\) - entièrement contenu dans \( U \).
Pour tout point \( y \) appartenant à un ouvert \( U \), il est toujours possible de construire une petite "sphère" (ou un disque dans le plan, ou une boule dans un espace de dimension supérieure) entièrement incluse dans \( U \).
C’est cette propriété qui distingue les ensembles ouverts : chaque point possède un voisinage contenu dans l’ensemble, sans en atteindre la frontière.
Voici ci-dessous un exemple d’ensemble ouvert dans l’espace métrique \( \mathbb{R}^2 \).
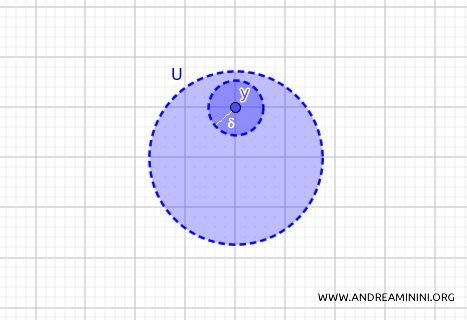
À l’inverse, les ensembles fermés sont des ensembles qui contiennent tous leurs points intérieurs ainsi que leurs points frontières - autrement dit, les adhérences des boules ouvertes.
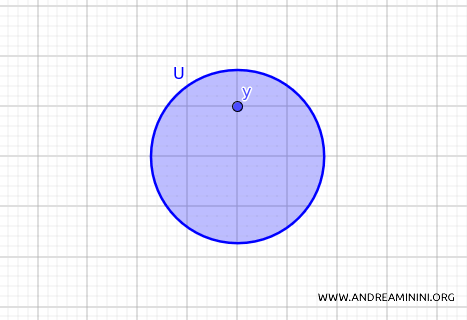
Ce critère illustre bien l’idée d’ouverture, en s’appuyant sur la notion de "proximité intérieure" de chaque point par rapport à l’ensemble.
Types de métriques
Les topologies induites par des métriques peuvent être construites à partir de différentes notions de distance, pas seulement à partir de la distance euclidienne (circulaire).
Voici quelques-unes des métriques les plus courantes sur le plan \( \mathbb{R}^2 \) :
- Métrique euclidienne (ou standard)
Cette métrique engendre des ensembles ouverts de forme circulaire, appelés boules ouvertes. Elle induit la topologie usuelle sur \( \mathbb{R}^2 \). $$ d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} $$
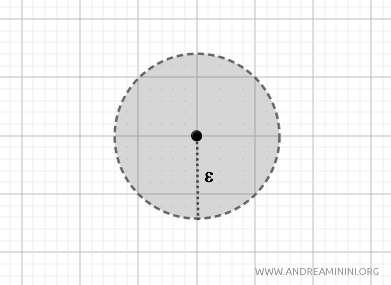
- Métrique du taxi (ou distance de Manhattan)
Dans ce cas, les boules ouvertes ont la forme d’un losange centré en \( p \). Cette métrique induit également la topologie usuelle sur \( \mathbb{R}^2 \). $$ d_T(p, q) = |p_1 - q_1| + |p_2 - q_2|. $$
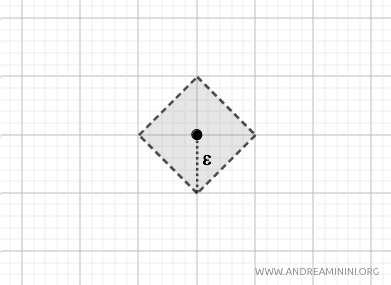
- Métrique du maximum
Avec cette métrique, les boules ouvertes sont des carrés centrés en \( p \), de côté \( 2\varepsilon \). Elle induit elle aussi une topologie sur \( \mathbb{R}^2 \).
$$ d_M(p, q) = \max\{|p_1 - q_1|, |p_2 - q_2|\} $$
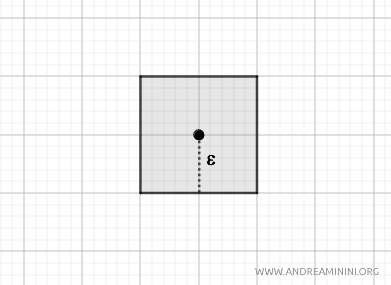
Bien que ces trois métriques donnent naissance à des boules ouvertes de géométries distinctes (cercle, losange, carré), elles induisent toutes une topologie métrique sur \( \mathbb{R}^2 \).
Remarques complémentaires
Voici quelques observations supplémentaires concernant les topologies induites par des métriques :
- Théorème : comparaison de topologies métriques
Soient \(d\) et \(d'\) deux métriques définies sur un même ensemble \(X\), induisant respectivement les topologies \(\mathcal{T}\) et \(\mathcal{T}'\). On dit que \(\mathcal{T}'\) est plus fine que \(\mathcal{T}\) si, pour tout \(x \in X\) et tout \(\varepsilon > 0\), il existe un \(\delta > 0\) tel que : $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ où \(B_{d}(x, \varepsilon)\) et \(B_{d'}(x, \delta)\) désignent les boules ouvertes centrées en \(x\) selon les métriques \(d\) et \(d'\).
En termes simples, \(\mathcal{T}'\) est plus fine que \(\mathcal{T}\) si tout ouvert de la topologie induite par \(d\) contient au moins un ouvert de celle induite par \(d'\). - Théorème de la métrique bornée
Dans un espace métrique \( (X, d) \), on peut définir une nouvelle métrique bornée par \( d'(x, y) = \min(d(x, y), \varepsilon) \), avec \(\varepsilon > 0\). Cette métrique engendre la même topologie que \( d \), ce qui signifie que les ensembles ouverts qu’elles définissent sont identiques.