Distance entre ensembles

La distance entre deux ensembles $A$ et $B$, dans un espace métrique $(X, d)$, est définie comme la plus petite distance possible entre un point de $A$ et un point de $B$ : $$ d(A, B) = \inf \{ d(a, b) \mid a \in A \ , \ b \in B \}, $$ où $d(a, b)$ désigne la distance entre les points $a$ et $b$ selon la métrique $d$, et $\inf$ désigne l’infimum, c’est-à-dire la borne inférieure de l’ensemble de ces distances.

Pour déterminer cette distance, on considère tous les couples possibles formés d’un point de $A$ et d’un point de $B$, puis on cherche la plus petite distance entre eux.

Autrement dit, la distance entre deux ensembles correspond à la valeur minimale que peuvent atteindre les distances entre leurs éléments respectifs.

Remarque : La distance entre deux ensembles mesure à quel point les éléments des deux ensembles peuvent être proches l’un de l’autre, sans pour autant impliquer qu’ils se touchent ou qu’ils aient un point commun.

Quand la distance vaut-elle zéro ?

Une distance nulle, $d(A, B) = 0$, signifie que certains points de $A$ et de $B$ peuvent être arbitrairement proches. Cela ne garantit toutefois ni qu’ils coïncident, ni que les ensembles se recouvrent.

Il est donc tout à fait possible que $d(A, B) = 0$ même si les ensembles sont disjoints, c’est-à-dire lorsque $A \cap B = \emptyset$.

Exemple illustratif

Considérons deux ensembles $A$ et $B$ dans un espace métrique défini sur la droite réelle, muni de la distance usuelle $d(x_1, x_2) = |x_1 - x_2|$.

Examinons trois situations différentes :

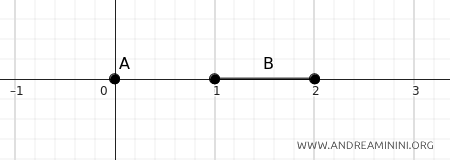
A] Cas 1

Si $A = \{0\}$ et $B = [1, 2]$, alors la distance entre eux est égale à $1$.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(0, 1) = 1 $$

Le point $0$, appartenant à $A$, est situé exactement à une unité du point le plus proche de $B$, à savoir $1$.

distancia entre un punto aislado y un intervalo cerrado

B] Cas 2

Si $A = [0, 1]$ et $B = [1, 2]$, la distance entre les deux ensembles est nulle.

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(1, 1) = 0 $$

Ici, les ensembles sont adjacents et partagent le point $1$, ce qui rend leur distance égale à zéro.

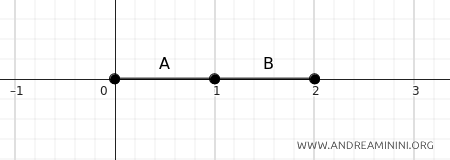
intervalos cerrados que se intersectan en un solo punto

Ils ne sont pas disjoints, puisqu’ils ont un point en commun :

$$ A \cap B = \{ 1 \} $$

C] Cas 3

Si $A = (0, 1)$ et $B = (1, 2)$, la distance est également nulle :

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} $$

Bien que ces intervalles ouverts ne partagent aucun point - le point $1$ n’appartient ni à $A$ ni à $B$ - la distance entre eux est toujours égale à zéro.

$$ A \cap B = \emptyset $$

La raison en est que l’on peut choisir des points $a \in A$ et $b \in B$ aussi proches que l’on veut du point $1$, sans jamais l’atteindre, de sorte que $|a - b|$ peut être rendu arbitrairement petit.

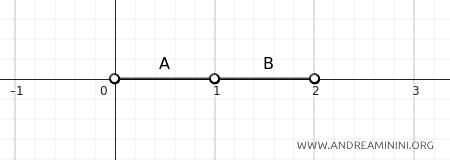
intervalos abiertos que no se tocan pero cuya distancia es cero

Les éléments de $A$ peuvent s’approcher de $1$ par la gauche, tandis que ceux de $B$ peuvent en faire autant par la droite - mais dans les deux cas, sans jamais inclure $1$, puisque les intervalles sont ouverts.

La distance entre $A$ et $B$ est donc :

$$ d(A, B) = \inf \{ |a - b| \mid a \in A, b \in B \} = |1 - 1| = 0 $$

En résumé, même si $A$ et $B$ ne se touchent pas et n’ont aucun point en commun, leurs éléments peuvent se rapprocher indéfiniment.

Pour cette raison, leur distance est égale à $0$.

Remarque : Le fait que deux ensembles aient une distance nulle ne signifie ni qu’ils sont identiques, ni qu’ils se rencontrent. Cette notion traduit uniquement la proximité potentielle de leurs éléments, indépendamment de toute intersection réelle.

Et ainsi de suite.