Distance de Levenshtein

Cette métrique trouve des applications directes dans des domaines tels que les correcteurs orthographiques, où elle permet de comparer des mots similaires et de proposer des suggestions de correction. Elle constitue un outil classique pour mesurer la similarité entre chaînes de caractères.

Son calcul repose sur la construction d’une matrice dont chaque cellule indique le coût minimal pour transformer un préfixe de la première chaîne en un préfixe de la seconde, en accumulant étape par étape le plus petit nombre d’opérations possible.

Contrairement à la distance de Hamming, la distance de Levenshtein s’applique également à des chaînes de longueurs différentes.

Exemple concret

Considérons les chaînes \( s \) et \( t \) :

$$ s = "kitten" $$

$$ t = "sitting" $$

Nous cherchons à déterminer la distance de Levenshtein entre ces deux mots, c’est-à-dire le nombre minimal d’éditions (insertions, suppressions ou substitutions) nécessaires pour transformer « kitten » en « sitting ».

1. Substitution
   Remplacer \( k \) par \( s \) : $$ "kitten" \rightarrow "sitten" $$
2. Substitution
   Remplacer \( e \) par \( i \) : $$ "sitten" \rightarrow "sittin" $$
3. Insertion
   Ajouter un \( g \) en fin de chaîne : $$ "sittin" \rightarrow "sitting" $$

Au total, trois opérations sont nécessaires (deux substitutions et une insertion) ; la distance de Levenshtein entre « kitten » et « sitting » est donc égale à 3.

Pour modéliser ce processus, on construit une matrice de dimensions \( (m+1) \times (n+1) \), où \( m \) désigne la longueur de « kitten » (6) et \( n \) celle de « sitting » (7).

On ajoute une ligne et une colonne supplémentaires afin de représenter les transformations à partir ou vers la chaîne vide.

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1
i	2
t	3
t	4
e	5
n	6

La cellule \( (0, j) \) représente le coût de transformation d’une chaîne vide en le préfixe de « sitting » de longueur \( j \) ; ce coût croît linéairement de 0 à 7.

Symétriquement, la cellule \( (i, 0) \) indique le coût pour transformer le préfixe de « kitten » de longueur \( i \) en une chaîne vide, ce coût augmentant de 0 à 6.

Pour chaque cellule \( (i, j) \), le coût minimal se détermine en évaluant trois possibilités :

1. supprimer un caractère de « kitten » (coût de la cellule du dessus, \( +1 \)) ;
2. insérer un caractère dans « kitten » (coût de la cellule de gauche, \( +1 \)) ;
3. remplacer un caractère (coût de la cellule diagonale) ; si les caractères sont identiques, aucun coût supplémentaire n’est ajouté.

On complète ensuite la matrice pas à pas :

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1	1	2	3	4	5	6	7
i	2	2	1	2	3	4	5	6
t	3	3	2	1	2	3	4	5
t	4	4	3	2	1	2	3	4
e	5	5	4	3	2	2	3	4
n	6	6	5	4	3	3	2	3

Par exemple, transformer une chaîne vide en « s », « si », « sit », etc., exige une opération supplémentaire pour chaque caractère ajouté.

De manière similaire, transformer « k », « ki », « kit », etc., en une chaîne vide entraîne un coût qui croît d’une unité à chaque caractère supprimé.

• La cellule (1,1) indique le coût pour remplacer « k » par « s », soit 1, puisqu’une seule substitution est nécessaire.
  
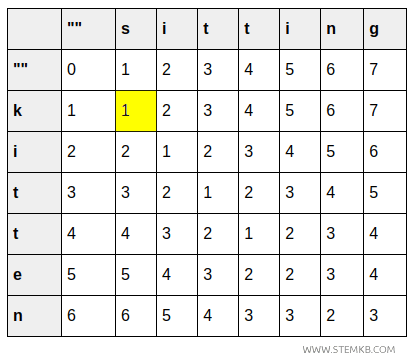
• La cellule (2,2) correspond au coût de transformation de « ki » en « si », inchangé à 1 puisque le deuxième caractère (i) est identique.
• La cellule (3,3) représente le coût pour passer de « kit » à « sit », toujours 1, la troisième lettre (t) restant la même.
• La cellule (4,4) donne le coût pour transformer « kitt » en « sitt », encore égal à 1, car le quatrième caractère (t) ne change pas.
• La cellule (5,5) affiche un coût de 2 pour passer de « kitte » à « sitti » en raison d’une substitution (e→i).
  
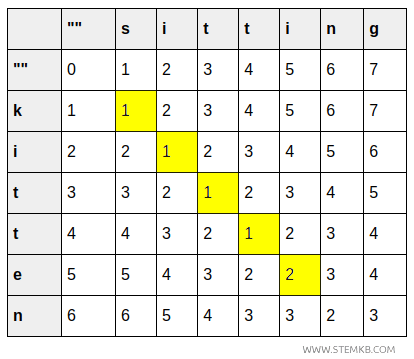
• La cellule (6,6) indique le coût pour convertir « kitten » en « sittin », inchangé à 2, car le dernier caractère (n) est identique.
• La cellule (6,7) montre un coût total de 3 pour passer de « kitten » à « sitting », impliquant l’insertion d’un g final.
  

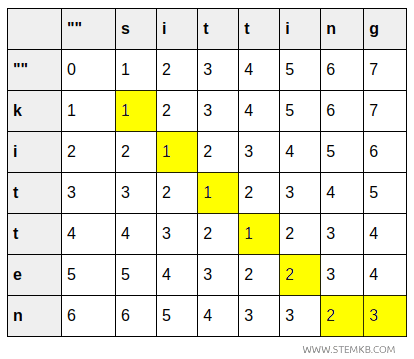
On atteint ainsi la cellule finale, qui contient le coût total cumulé.

La cellule en bas à droite \( (6,7) \) donne le coût minimal pour transformer « kitten » en « sitting » : un total de 3.

Ce résultat correspond exactement à la distance de Levenshtein calculée : 2 substitutions et 1 insertion.

Topologie induite par la distance de Levenshtein

La distance de Levenshtein induit une structure d’espace métrique sur l’ensemble des chaînes de caractères, à l’instar de la distance de Hamming, car elle satisfait les propriétés fondamentales qui définissent une métrique.

1. Non-négativité : La distance de Levenshtein entre deux chaînes \( x \) et \( y \) est toujours supérieure ou égale à zéro, et \( D_L(x, y) = 0 \) si et seulement si \( x = y \). Autrement dit, aucune opération n’est requise pour transformer une chaîne en elle-même, et la distance est donc nulle uniquement lorsque les deux chaînes sont identiques.
2. Symétrie : La distance de Levenshtein est symétrique ; ainsi \( D_L(x, y) = D_L(y, x) \). Le nombre d’éditions nécessaires pour passer de \( x \) à \( y \) est le même que pour passer de \( y \) à \( x \), puisque les opérations autorisées (insertion, suppression, substitution) sont réversibles.
3. Inégalité triangulaire : On a toujours \( D_L(x, z) \leq D_L(x, y) + D_L(y, z) \). En d’autres termes, la distance directe entre \( x \) et \( z \) n’excède jamais la somme des distances obtenues en passant par une chaîne intermédiaire \( y \).

Ces propriétés garantissent que la distance de Levenshtein définit un espace métrique sur l’ensemble des chaînes.

En tant que métrique valide, elle permet également de définir la topologie métrique induite associée à cet espace.

Pour un rayon \( r \) et une chaîne \( x \), on appelle boule ouverte centrée en \( x \) l’ensemble des chaînes \( y \) telles que leur distance à \( x \) soit strictement inférieure à \( r \) :

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$

L’ensemble de ces boules ouvertes constitue une base de la topologie induite.

Ce cadre est particulièrement pertinent dans les domaines où la notion de « proximité » entre chaînes est essentielle. Par exemple, dans un système de correction orthographique automatique, un mot dont la distance de Levenshtein à un terme du dictionnaire est faible pourra être suggéré comme correction.

Dans cette optique, les chaînes sont considérées comme des points d’un espace métrique, et la topologie induite sert à analyser leur proximité d’un point de vue formel.

Exemple

Considérons l’ensemble \( X \) constitué de chaînes de trois caractères :

$$ X = \{"cat", "bat", "cut"\} $$

On définit une base de la topologie en prenant les boules ouvertes de rayon \( r = 2 \) centrées sur chaque élément de \( X \) :

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$ 

Chaque boule ouverte contient toutes les chaînes qui diffèrent d’un seul caractère de la chaîne centrale, selon la distance de Levenshtein.

Remarque : Avec un rayon \( r = 2 \), on inclut uniquement les chaînes dont la distance est strictement inférieure à 2. Ainsi, $$ B(x, 2) = \{ y \mid D_L(x, y) < 2 \} $$. Pour définir un ensemble fermé englobant les points frontières, on utiliserait l’inégalité large : $$ C(x, 2) = \{ y \mid D_L(x, y) \le 2 \} $$

Examinons maintenant les boules ouvertes de rayon \( 2 \) centrées sur chaque élément de \( X \) :

1. Boule ouverte centrée sur "cat" $$ B("cat", 2) = \{"cat", "bat"\} $$ Ces chaînes peuvent être obtenues l’une à partir de l’autre par une seule substitution de caractère.
2. Boule ouverte centrée sur "bat" $$ B("bat", 2) = \{"bat", "cat"\} $$ Contient toutes les chaînes transformables en « bat » en une seule opération.
3. Boule ouverte centrée sur "cut" $$ B("cut", 2) = \{"cut"\} $$ Aucune autre chaîne de \( X \) n’est à distance 1 de « cut », cette boule ne contient donc qu’elle-même.

Les ensembles \( B("cat", 2) \), \( B("bat", 2) \) et \( B("cut", 2) \) forment une base de la topologie induite par la distance de Levenshtein avec rayon \( r = 1 \).

À partir de cette base, on peut générer tous les autres ouverts comme unions arbitraires de ces boules ouvertes.

Par exemple, l’union de \( B("bat", 1) \) et \( B("cut", 1) \) est :

$$ B("bat", 1) \cup B("cut", 1) $$

Comme \( B("cat", 2) = \{"cat", "bat"\} \) et \( B("cut", 2) = \{"cut"\} \), on obtient :

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat"\} \cup \{"cut"\} $$

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat", "cut"\} $$

Cet ensemble est donc également un ouvert de la topologie induite.

Par cette construction, on obtient une topologie métrique sur \( X \) induite par la distance de Levenshtein, dans laquelle tout ouvert peut s’exprimer comme union de ces éléments de base.

Et ainsi de suite.