Équivalence métrique

Deux espaces métriques sont dits équivalents s’il existe une application $f : X \to Y$ satisfaisant les conditions suivantes :

Bijectivité : chaque élément de $X$ correspond à un et un seul élément de $Y$, et réciproquement.
Isométrie : pour tous $x_1, x_2 \in X$, la distance qui les sépare dans $X$ est exactement égale à la distance entre leurs images $f(x_1)$ et $f(x_2)$ dans $Y$ : $$ d_X(x_1, x_2) = d_Y(f(x_1), f(x_2)) $$

Lorsqu’une telle application existe, on dit que $X$ et $Y$ sont isométriques, c’est-à-dire métriquement équivalents.

En termes généraux, l’équivalence métrique consiste à comparer deux espaces métriques $(X, d_X)$ et $(Y, d_Y)$ pour déterminer s’ils sont, du point de vue de la mesure des distances entre points, essentiellement identiques.

Si deux espaces métriques sont isométriques, ils possèdent la même topologie : autrement dit, leurs ensembles ouverts - la « structure globale » de l’espace - coïncident. Cependant, la réciproque n’est pas toujours vraie.
Partager la même topologie ne suffit pas pour qu’il y ait isométrie : l’isométrie impose une condition plus forte que l’équivalence topologique, en exigeant la conservation exacte de toutes les distances, et pas seulement de la structure des ouverts.

Exemple concret

Considérons les deux espaces métriques suivants :

$X = \{a, b, c\}$, avec la métrique $d_X$ définie par : $$ d_X(a, b) = 1, \quad d_X(b, c) = 2, \quad d_X(a, c) = 3 $$
$Y = \{p, q, r\}$, avec la métrique $d_Y$ donnée par : $$ d_Y(p, q) = 1, \quad d_Y(q, r) = 2, \quad d_Y(p, r) = 3 $$

Définissons $f : X \to Y$ par :

$$ f(a) = p, \quad f(b) = q, \quad f(c) = r $$

Vérifions la conservation des distances :

$d_X(a, b) = 1$ et $d_Y(f(a), f(b)) = d_Y(p, q) = 1$
$d_X(b, c) = 2$ et $d_Y(f(b), f(c)) = d_Y(q, r) = 2$
$d_X(a, c) = 3$ et $d_Y(f(a), f(c)) = d_Y(p, r) = 3$

Puisque toutes les distances sont préservées, $f$ est une isométrie. Les espaces $X$ et $Y$ sont donc isométriques, c’est-à-dire équivalents du point de vue métrique.

Exemple 2

Dans le plan, la métrique du taxi ($d_T$) et la métrique euclidienne standard ($d$) induisent la même topologie : elles engendrent les mêmes ensembles ouverts.

Mais ces deux espaces métriques sont-ils pour autant isométriques ?

Avec la métrique du taxi, la distance entre $(x_1, y_1)$ et $(x_2, y_2)$ est définie par :

$$ d_T((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2| $$

Cette métrique mesure la distance en suivant des déplacements horizontaux et verticaux, à la manière d’un trajet sur une grille urbaine.

En revanche, la métrique euclidienne mesure la distance en ligne droite :

$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$

Supposons qu’il existe une application $f : \mathbb{R}^2 \to \mathbb{R}^2$ préservant les distances pour les deux métriques. Considérons $A = (1, 1)$ et $B = (2, 2)$.

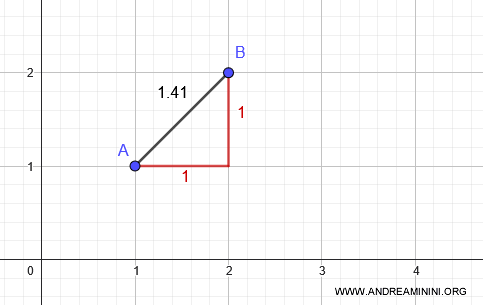
comparaison graphique entre la métrique du taxi et la métrique euclidienne

Selon la métrique du taxi :

$$ d_T((2, 2), (1, 1)) = |2 - 1| + |2 - 1| = 2 $$

Avec la métrique euclidienne :

$$ d((1, 1), (2, 2)) = \sqrt{(1 - 2)^2 + (1 - 2)^2} = \sqrt{2} \approx 1.41 $$

Les distances étant différentes, il ne peut exister d’isométrie préservant simultanément ces deux métriques. Ainsi, le plan muni de la métrique du taxi n’est pas isométrique au plan muni de la métrique euclidienne.

En résumé, bien que ces deux métriques induisent la même topologie - elles définissent les mêmes ensembles ouverts - , elles ne sont pas isométriques.

Et ainsi de suite.