Théorème de la métrique bornée

Dans un espace métrique $ (X, d) $, on peut définir une nouvelle métrique bornée donnée par $ d'(x, y) = \min(d(x, y), 1) $, qui induit exactement la même topologie que la métrique d’origine $ d $. Autrement dit, les ensembles ouverts définis par $ d $ et ceux définis par $ d' $ sont identiques.

En d’autres termes, la fonction $ d'(x, y) $ est obtenue à partir de la métrique initiale $ d(x, y) $, selon la formule :

$$ d'(x, y) = \min(d(x, y), 1) $$

La fonction $ d' $ coïncide avec $ d $ tant que $ d(x, y) < 1 $, mais toute distance supérieure ou égale à $1$ est « coupée » à cette valeur. La métrique $ d' $ est donc uniformément bornée par 1.

Malgré cette borne supérieure, la topologie induite par $ d' $ est exactement la même que celle engendrée par $ d $. Ainsi, la structure topologique de l’espace reste inchangée.

Remarque : Le nombre $1$ peut être remplacé, de manière générale, par n’importe quel $\varepsilon > 0$ : $$ d'(x, y) = \min(d(x, y), \varepsilon) $$ Dans ce cas, les distances sont bornées par $\varepsilon$, mais la topologie engendrée par $ d' $ reste inchangée. Pour simplifier, nous nous concentrerons ici sur le cas particulier $\varepsilon = 1$.

Un exemple illustratif
Démonstration

Un exemple illustratif

Considérons l’espace $ \mathbb{R} $, muni de la métrique usuelle :

$$ d(x, y) = |x - y| $$

Définissons une nouvelle métrique bornée de la forme suivante :

$$ d'(x, y) = \min(|x - y|, 1) $$

Avec cette définition, aucune distance ne peut dépasser la valeur $1$.

Par exemple, si $ x = 2 $ et $ y = 5 $, on a $ d(2, 5) = |2 - 5| = 3 $, alors que la métrique bornée donne $ d'(2, 5) = \min(3, 1) = 1 $. En revanche, si $ x = 2 $ et $ y = 2{,}5 $, alors $ d'(2, 2.5) = \min(|2 - 2.5|, 1) = 0.5 $, ce qui correspond à la métrique initiale, puisque $ |2 - 2.5| < 1 $. Dans ce cas, on a bien $ d = d' = 0.5 $. $$ \begin{array}{|c|c|c|c|} \hline x & y & d & d' \\ \hline 2 & 5 & 3 & 1 \\ \hline 2 & 2.5 & 0.5 & 0.5 \\ \hline 6 & 8 & 2 & 1 \\ \hline \end{array} $$

La métrique $ d' $ tronque toutes les distances supérieures à $1$, mais la notion de proximité - et donc les ensembles ouverts - demeure inchangée. Les deux métriques engendrent donc la même topologie.

Pourquoi la topologie reste-t-elle inchangée ?

Dans une topologie métrique, les ouverts sont définis comme des unions (potentiellement infinies) de boules ouvertes.

Bien que les boules associées à $ d' $ soient plus petites, tout ouvert de la topologie de $ d $ peut être exprimé comme une union appropriée de boules ouvertes pour $ d' $.

Par exemple, considérons la boule $ B_d(3, 2) $, centrée en $3$ et de rayon $2$.

Elle est définie comme l’ensemble des $ y \in \mathbb{R} $ tels que la distance à $3$ est strictement inférieure à $2$ :

$$ B_d(3, 2) = \{y \in \mathbb{R} \mid d(3, y) < 2\} $$

En utilisant la définition usuelle $ d(x, y) = |x - y| $, on a :

$$ |3 - y| < 2 \Rightarrow 1 < y < 5 $$

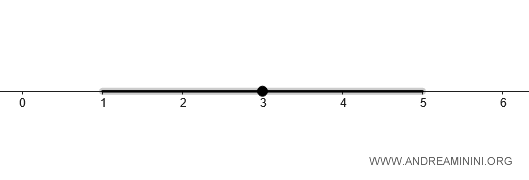
Donc : $$ B_d(3, 2) = (1, 5) $$ un intervalle ouvert de longueur $4$, centré en $3$.

example

Pour recouvrir cet intervalle en utilisant la métrique $ d' $, il suffit de prendre l’union de deux boules ouvertes plus petites :

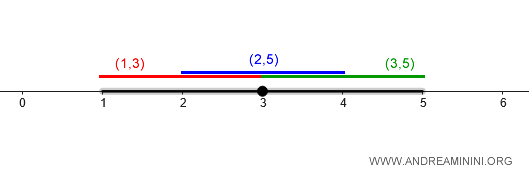
$$ B_{d'}(2, 1) \cup B_{d'}(3, 1) $$

La première couvre l’intervalle $ (1, 3) $, la seconde $ (2, 4) $ ; leur union couvre ainsi l’ensemble $ (1, 5) $.

example

Ce simple exemple montre que, par un recouvrement adapté, les boules ouvertes de $ d' $ permettent de reconstruire tous les ouverts définis par $ d $. Ainsi, les deux métriques induisent exactement la même topologie.

Démonstration

Pour établir que $ d' $ induit la même topologie que $ d $, commençons par vérifier que $ d' $ satisfait bien les axiomes d’une métrique :

$ d'(x, y) \geq 0 $ (positivité),
$ d'(x, y) = 0 $ si et seulement si $ x = y $ (identité des indiscernables),
$ d'(x, y) = d'(y, x) $ (symétrie),
$ d' $ satisfait l’inégalité triangulaire.

L’inégalité triangulaire s’établit comme suit :

Si $ d(x, y) \geq 1 $ ou $ d(y, z) \geq 1 $, alors $ d'(x, y) + d'(y, z) \leq 2 $, et comme $ d'(x, z) \leq 1 $, on a bien : $$ d'(x, z) \leq d'(x, y) + d'(y, z) $$
Si $ d(x, y) < 1 $ et $ d(y, z) < 1 $, alors $ d' $ coïncide avec $ d $ sur les trois points concernés. Or, $ d $ étant une métrique, elle vérifie déjà l’inégalité triangulaire.

Ayant établi que $ d' $ est bien une métrique, il reste à prouver que les topologies induites par $ d $ et $ d' $, notées $ T $ et $ T' $, sont identiques. Il suffit pour cela de démontrer les deux inclusions :

$ T \subseteq T' $,
$ T' \subseteq T $.

A] Inclusion $ T \subseteq T' $

Cette inclusion découle immédiatement des faits suivants :

Si $ r \leq 1 $, alors : $$ B_d(x, r) = B_{d'}(x, r) $$
Si $ r > 1 $, alors : $$ B_{d'}(x, r) \subseteq B_d(x, r) $$ ce qui signifie que toute boule de $ d' $ est incluse dans une boule de $ d $, donc est ouverte dans la topologie de $ d $.

B] Inclusion $ T' \subseteq T $

La réciproque est également vraie :

Si $ r \leq 1 $, alors : $$ B_d(x, r) = B_{d'}(x, r) $$
Si $ r > 1 $, alors la boule $ B_d(x, r) $ peut être recouverte par une réunion (finie ou dénombrable) de boules de rayon $ \varepsilon \leq 1 $, ouvertes dans la topologie de $ d' $ :

$$ B_d(x, r) = \bigcup_{i} B_{d'}(x_i, \varepsilon) $$

Conclusion

Puisque chaque topologie est incluse dans l’autre, il s’ensuit que $ T = T' $. Cela montre que les métriques $ d $ et $ d' $ induisent exactement la même structure topologique sur $ X $.