Théorème de comparaison entre topologies induites par des métriques

Soient $d$ et $d'$ deux métriques définies sur un ensemble $X$, et soient $\mathcal{T}$ et $\mathcal{T}'$ les topologies qu’elles induisent respectivement. La topologie $\mathcal{T}'$ est dite plus fine que $\mathcal{T}$ si, et seulement si, pour tout $x \in X$ et tout $\varepsilon > 0$, il existe un $\delta > 0$ tel que : $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ où $B_d(x, \varepsilon)$ et $B_{d'}(x, \delta)$ désignent les boules ouvertes de centre $x$, de rayons respectifs $\varepsilon$ et $\delta$, définies selon les métriques $d$ et $d'$.

Autrement dit, si l’on considère deux façons différentes de mesurer les distances sur un même ensemble $X$ - c’est-à-dire deux métriques $d$ et $d'$ - chacune d’elles induit une topologie propre, c’est-à-dire une collection d’ouverts :

La topologie $\mathcal{T}$, induite par la métrique $d$ ;
La topologie $\mathcal{T}'$, induite par la métrique $d'$.

Le théorème établit que $\mathcal{T}'$ est plus fine que $\mathcal{T}$ - c’est-à-dire qu’elle contient tous les ouverts de $\mathcal{T}$, voire davantage - si et seulement si tout ouvert de $\mathcal{T}$ contient au moins un ouvert appartenant à $\mathcal{T}'$.

Ce critère fournit un outil rigoureux pour comparer les topologies et montre comment le choix de la métrique influe sur la structure des ensembles ouverts.

Un exemple concret
Démonstration du théorème

Un exemple concret

Considérons le plan cartésien $X = \mathbb{R}^2$, muni de deux métriques distinctes :

Métrique euclidienne : $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$. Les boules ouvertes correspondantes sont des disques de rayon $\varepsilon$ : $$ B_d((x, y), \varepsilon) = \{(u, v) \in \mathbb{R}^2 : \sqrt{(u - x)^2 + (v - y)^2} < \varepsilon\} $$
Métrique discrète : $d'((x_1, y_1), (x_2, y_2)) = \begin{cases} 0 & \text{si } (x_1, y_1) = (x_2, y_2), \\ 1 & \text{si } (x_1, y_1) \neq (x_2, y_2) \end{cases}$. Les boules ouvertes associées s’écrivent : \[ B_{d'}((x, y), \delta) = \begin{cases} \{(x, y)\} & \text{si } \delta \leq 1, \\ X & \text{si } \delta > 1. \end{cases} \]

Montrons que la topologie discrète est plus fine que la topologie euclidienne.

D’après le théorème :

$$ \mathcal{T}' \text{ est plus fine que } \mathcal{T} \iff \forall x \in X, \forall \varepsilon > 0, \ \exists \ \delta > 0 \text{ tel que } B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

Soit un point quelconque $P = (x_0, y_0) \in \mathbb{R}^2$ et un rayon $\varepsilon > 0$. La boule $B_d(P, \varepsilon)$, pour la métrique euclidienne, est un disque ouvert centré en $P$.

Pour la métrique discrète, les boules prennent la forme suivante :

Si $\delta \leq 1$, alors $B_{d'}(P, \delta) = \{P\}$
Si $\delta > 1$, alors $B_{d'}(P, \delta) = X$

Dans cette topologie, tout singleton est ouvert.

En prenant $\delta = 1$, on a $B_{d'}(P, \delta) = \{P\}$. Comme $P \in B_d(P, \varepsilon)$, il en résulte : $$ B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon) $$

Prenons par exemple le point $P = (1, 2) \in \mathbb{R}^2$. Dans la topologie euclidienne, la boule de rayon $\varepsilon = 0{,}4$ centrée en $P$ est un ouvert.
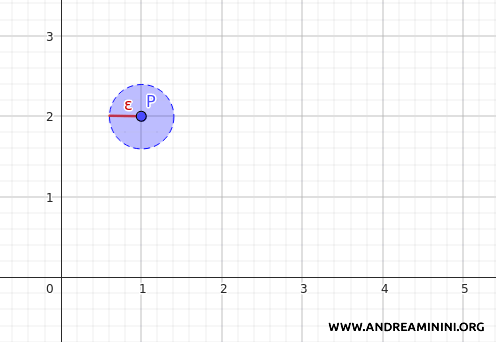
example
Dans la topologie discrète, le singleton $\{P\} = \{(1, 2)\}$ est ouvert par définition. Et comme $\{P\} \subseteq B_d(P, \varepsilon)$, la condition du théorème est satisfaite. Cet argument s’applique à tout point du plan, ce qui montre que chaque ouvert euclidien contient au moins un ouvert de la topologie discrète.

En définitive, on a bien : la topologie discrète ($\mathcal{T}'$) est plus fine que la topologie euclidienne ($\mathcal{T}$), car pour tout point $P$ et tout rayon $\varepsilon > 0$, il existe un $\delta > 0$ (par exemple $\delta = 1$) tel que $B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon)$.

Démonstration du théorème

La preuve repose sur l’équivalence logique des deux affirmations suivantes :

Si $\mathcal{T}'$ est plus fine que $\mathcal{T}$, alors pour tout $x \in X$ et tout $\varepsilon > 0$, il existe $\delta > 0$ tel que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.
Réciproquement, si cette inclusion est vérifiée pour tout $x \in X$ et tout $\varepsilon > 0$, alors $\mathcal{T}'$ est plus fine que $\mathcal{T}$.

La démonstration se décompose en deux implications.

A] Première implication

Supposons que $\mathcal{T}'$ est plus fine que $\mathcal{T}$. Alors, pour tout $x \in X$ et tout $\varepsilon > 0$, il existe $\delta > 0$ tel que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.

Par définition, si $\mathcal{T}'$ est plus fine que $\mathcal{T}$, alors tout ouvert de $\mathcal{T}$ est aussi un ouvert de $\mathcal{T}'$. En particulier, chaque boule $B_d(x, \varepsilon)$ est ouverte dans $\mathcal{T}'$.
Or, pour qu’un ensemble soit ouvert dans $\mathcal{T}'$, il doit contenir une boule $B_{d'}(x, \delta)$ centrée en $x$.
Il en découle que $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ pour un certain $\delta > 0$.

B] Seconde implication

Supposons maintenant que, pour tout $x \in X$ et tout $\varepsilon > 0$, il existe un $\delta > 0$ tel que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$. Montrons que cela implique que $\mathcal{T}'$ est plus fine que $\mathcal{T}$.

Soit $U$ un ouvert de $\mathcal{T}$. Par définition, $U$ peut s’écrire comme une union de boules ouvertes $B_d(x, \varepsilon)$.
Pour tout $x \in U$, il existe une boule $B_d(x, \varepsilon) \subseteq U$.
D’après l’hypothèse, il existe $\delta > 0$ tel que $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) \subseteq U$.
On en conclut que chaque point de $U$ possède un voisinage ouvert dans $\mathcal{T}'$ contenu dans $U$, ce qui montre que $U$ est ouvert dans $\mathcal{T}'$.

La démonstration de l’équivalence est ainsi complète.

Et ainsi de suite.