Connexité en topologie

En topologie, un espace est dit connexe s’il ne peut pas être décomposé en deux ensembles ouverts disjoints et non vides. La connexité est donc la propriété topologique qui exprime l’impossibilité de séparer l’espace en deux parties ouvertes indépendantes.

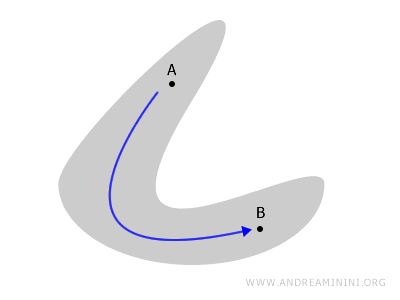
La connexité décrit la manière dont les différentes parties d’un espace topologique forment un tout indissociable ou, au contraire, peuvent être séparées.

Il s’agit d’une propriété topologique fondamentale, car elle est définie exclusivement à partir de la notion d’ensembles ouverts.

Ce concept joue un rôle central en topologie, au même titre que la continuité.

La connexité est essentielle dans de nombreux domaines des mathématiques, car elle permet de comprendre la structure globale des espaces et les relations entre leurs composantes. Elle intervient notamment dans la classification et l’analyse des espaces topologiques.

Exemple pratique

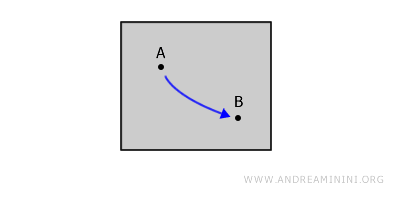
Qu’il s’agisse d’une figure plane ou d’un polyèdre, un espace est dit connexe par chemins s’il existe un chemin continu reliant deux points quelconques A et B de cet espace, sans jamais en sortir.

En revanche, si l’espace peut être scindé en plusieurs parties isolées les unes des autres, il est dit non connexe, ou encore disconnexe.

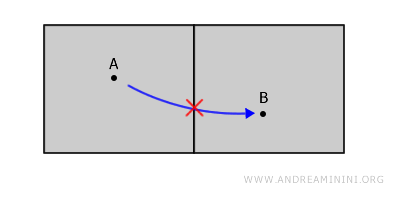
Dans la configuration suivante, l’espace est séparé en deux parties disjointes, et tout chemin reliant les points A et B devrait nécessairement sortir de l’espace considéré.

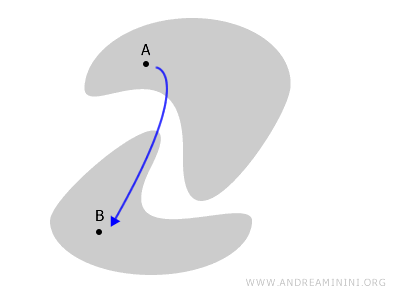
Il est utile d’approfondir cette idée à l’aide d’un exemple concret d’espace disconnexe.

Quand parle-t-on d’espace disconnexe ?

Un exemple intuitif d’espace disconnexe est celui de deux pièces distinctes d’un même bâtiment, séparées par un mur. Chacune des pièces constitue un ensemble ouvert, et ces deux ensembles sont disjoints.

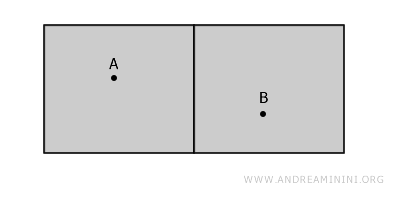
Bien que les pièces paraissent proches, elles ne sont pas connexes, car tout trajet reliant un point A à un point B impose de traverser le mur, qui ne fait pas partie de l’espace considéré.

Il est donc essentiel de rappeler que les frontières ne font pas partie des ensembles ouverts.

Connexité locale

On dit qu’un espace est localement connexe lorsque tout point admet un voisinage ouvert qui est connexe. Autrement dit, chaque point est contenu dans un sous-ensemble ouvert connexe.

Considérons par exemple un espace formé de plusieurs ensembles ouverts disjoints, comme les deux pièces distinctes d’un bâtiment.

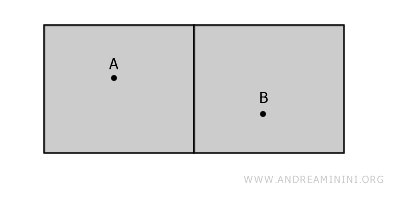
Bien que l’espace soit globalement disconnexe et qu’il soit impossible de relier les points A et B sans franchir les murs, chaque point pris isolément possède un voisinage connexe.

Ainsi, autour du point A, il existe un sous-ensemble ouvert connexe qui illustre la notion de connexité locale.

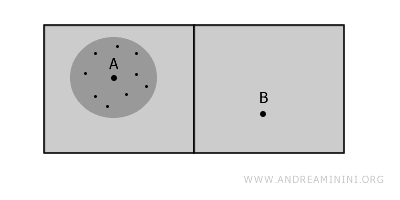
De la même manière, le point B admet lui aussi un voisinage connexe.

Types de connexité

On distingue plusieurs formes de connexité en topologie, parmi lesquelles les plus importantes sont :

• Connexité topologique
  Un espace topologique \( X \) est dit connexe s’il est impossible de le décomposer en deux ensembles ouverts, disjoints et non vides dont la réunion est égale à \( X \). Il n’existe donc aucun moyen de « scinder » l’espace en deux régions ouvertes indépendantes.

  Exemple. L’intervalle (-1, 1) est connexe, tandis que l’union (-1, 0) ∪ (0, 1) ne l’est pas, car elle peut être écrite comme la réunion de deux ensembles ouverts, disjoints et non vides, à savoir (-1, 0) et (0, 1). Ces deux ensembles constituent une séparation de l’espace.

• Connexité par chemins (ou par arcs)
  Un espace topologique est dit connexe par chemins si, pour tout couple de points A et B, il existe un chemin continu reliant A à B et entièrement contenu dans l’espace. Tout espace connexe par chemins est connexe, mais la réciproque n’est pas toujours vraie.

  Par exemple, dans une région plane fermée, il est possible de relier n’importe quels points A et B par une courbe continue sans sortir de la région.
  
  Différence entre connexité par arcs et par chemins. La connexité par arcs est une forme plus restrictive : le chemin doit être injectif, c’est-à-dire qu’il ne repasse pas deux fois par le même point.

• Simple connexité
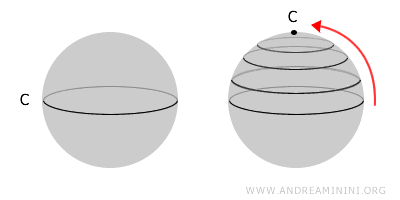
  Un espace est dit simplement connexe si toute boucle fermée qu’il contient peut être continûment déformée en un point. Un espace simplement connexe est toujours connexe, mais l’inverse n’est pas vrai. Formellement, cela signifie que toute boucle est homotope à une constante.

  Par exemple, une sphère est simplement connexe, car toute boucle tracée sur sa surface peut être contractée en un point. En revanche, un tore possède un trou central, ce qui empêche de contracter certaines boucles.
  
  
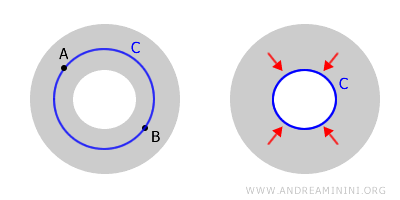
  Un espace connexe mais non simplement connexe est parfois qualifié de multiconnexe. L’espace annulaire en est un exemple classique.

Observations

Voici quelques remarques importantes :

• Dans \( \mathbb{R} \), les seuls sous-ensembles connexes sont les intervalles.