Tout sous-ensemble connexe est contenu dans une unique composante connexe de l’espace
Soient \( A \) et \( B \) deux sous-ensembles d’un espace topologique \( X \). On suppose que \( A \) est connexe et que \( A \subset B \). Si l’ensemble \( B \) peut être séparé en deux sous-ensembles \( B_1 \) et \( B_2 \) dans \( X \), alors \( A \) doit nécessairement être entièrement contenu dans l’un des deux: $$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
Autrement dit, un sous-ensemble connexe ne peut pas intersecter simultanément les deux parties d’une séparation.
Dès qu’un sous-ensemble connexe est inclus dans un ensemble qui se décompose en deux parties disjointes, il ne peut pas se répartir entre elles. Il doit rester intégralement dans une seule de ces parties.
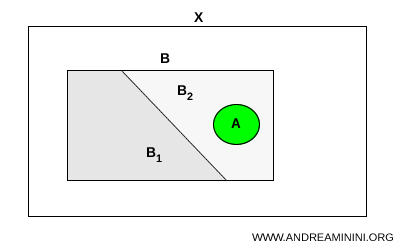
On peut s’en faire une image simple. Pensons à un sous-ensemble connexe comme à une corde continue placée dans une enveloppe. Si l’enveloppe est divisée en deux compartiments disjoints tandis que la corde reste intacte, celle-ci ne peut se trouver que dans l’un des deux. Pour occuper les deux compartiments, il faudrait la rompre. La notion de connexité traduit précisément cette impossibilité de « couper » l’ensemble en traversant une séparation.
Un exemple concret
Considérons l’espace topologique suivant:
$$ X = \mathbb{R} $$
et le sous-ensemble de \( X \):
$$ B = (-3,4) $$
Cet ensemble admet une séparation naturelle en deux sous-ensembles:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Ces deux sous-ensembles sont disjoints:
$$ B_1 \cap B_2 = \varnothing $$
et leur réunion redonne exactement l’ensemble initial:
$$ B_1 \cup B_2 = B $$
De plus, \( B_1 \) et \( B_2 \) sont ouverts pour la topologie de sous-espace induite sur \( B \).
Ils forment donc bien une séparation de \( B \) dans l’espace \( X \).
Considérons maintenant un sous-ensemble connexe de \( B \):
$$ A = (1,2) $$
On constate que \( A \subset B_2 \). Le sous-ensemble \( A \) est donc entièrement contenu dans l’une des deux parties de la séparation, conformément au résultat général.
Remarque. Si l’on considère au contraire \( A = (-1,1) \), on obtient $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Une telle situation est impossible, car \( B_1 \) et \( B_2 \) constituent une séparation de \( B \). Un sous-ensemble connexe de \( B \) ne peut pas être réparti entre les deux. Si cela était le cas, alors \( A \) admettrait lui-même une séparation, ce qui contredirait le fait fondamental que l’intervalle \( (-1,1) \) est connexe. Le point clé n’est donc pas une perte de connexité de \( (-1,1) \), mais l’impossibilité pour cet intervalle d’être contenu dans un ensemble séparé de cette manière.
Démonstration
Hypothèses
Soient \( A \) et \( B \) des sous-ensembles d’un espace topologique \( X \).
$$ A \subset X \quad \text{et} \quad B \subset X $$
On suppose que:
- \( A \) est connexe
- \( A \subset B \)
- \( B_1 \) et \( B_2 \) forment une séparation de \( B \) dans l’espace \( X \)
Proposition
Sous ces hypothèses, le sous-ensemble \( A \) est contenu dans \( B_1 \) ou dans \( B_2 \):
$$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
Démonstration
Par hypothèse, \( B_1 \) et \( B_2 \) constituent une séparation de \( B \) dans l’espace \( X \). On a en particulier:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) et \( B_2 \) sont ouverts pour la topologie de sous-espace induite sur \( B \)
Supposons, pour obtenir une contradiction, que \( A \) ne soit entièrement contenu ni dans \( B_1 \) ni dans \( B_2 \). On a alors:
$$ A \cap B_1 \neq \varnothing \qquad \text{et} \qquad A \cap B_2 \neq \varnothing $$
Comme \( A \subset B \), on peut écrire:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Les ensembles \( A \cap B_1 \) et \( A \cap B_2 \) sont disjoints, puisque \( B_1 \) et \( B_2 \) le sont.
De plus, comme \( B_1 \) et \( B_2 \) sont ouverts dans \( B \), les ensembles \( A \cap B_1 \) et \( A \cap B_2 \) sont ouverts dans la topologie de sous-espace induite sur \( A \).
Ainsi, \( A \cap B_1 \) et \( A \cap B_2 \) forment deux sous-ensembles disjoints, non vides et ouverts de \( A \). Ils définissent donc une séparation de \( A \) dans l’espace \( X \).
Ceci contredit l’hypothèse selon laquelle \( A \) est connexe.
On conclut alors que l’hypothèse initiale est fausse, et l’on obtient bien:
$$ A \subset B_1 \quad \text{ou} \quad A \subset B_2 $$
La proposition est ainsi démontrée.
Et ainsi de suite.