Théorème : caractérisation des espaces connexes à l’aide des ensembles ouverts et fermés

Un espace topologique \( X \) est dit connexe si, et seulement si, les seuls sous-ensembles de \( X \) qui sont à la fois ouverts et fermés (on dit aussi clopen) sont l’ensemble tout entier \( X \) et l’ensemble vide \( \emptyset \).

Autrement dit, un espace est connexe lorsqu’il ne peut pas être partitionné en deux sous-ensembles ouverts disjoints et non vides. Dans ce cas, les seuls ensembles clopen qu’il contient sont les deux cas triviaux : l’espace complet et l’ensemble vide.

Ce résultat fournit un critère fondamental de connexité topologique, qui permet de déterminer si un espace est connexe sans recourir à des notions plus avancées comme la connexité par arcs.

Interprétation

En topologie, un sous-ensemble qui est simultanément ouvert et fermé induit une séparation de l’espace : il décompose \( X \) en deux sous-ensembles ouverts, disjoints et non vides.

Si un tel sous-ensemble existe, l’espace peut être exprimé comme la réunion de deux ouverts disjoints et non vides, et il est alors non connexe (ou disconnexe dans certains ouvrages).

À l’inverse, si les seuls ensembles clopen de \( X \) sont \( X \) et \( \emptyset \), il n’existe aucune séparation topologique possible. L’espace \( X \) est donc connexe.

Remarque. Dans tout espace topologique, l’ensemble total \( X \) et l’ensemble vide \( \emptyset \) sont toujours à la fois ouverts et fermés. Ils constituent les deux ensembles clopen triviaux.

Exemple 1 : un espace fini non connexe

Considérons \( X = \{ a, b, c, d \} \) muni de la topologie \( T \) définie par les ensembles ouverts \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

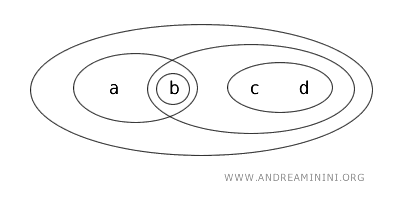
Dans ce cas, le sous-ensemble \( \{ a, b \} \) est clopen car il satisfait simultanément les deux conditions :

• il est ouvert, puisqu’il appartient explicitement à la famille des ensembles ouverts de la topologie \( T \) ;
• il est fermé, car son complémentaire \( X \setminus \{ a, b \} = \{ c, d \} \) est également un ouvert de \( T \).

On en déduit que l’espace topologique \( (X, T) \) est non connexe, puisqu’il contient un sous-ensemble propre non vide qui est clopen.

La présence d’un seul ensemble clopen non trivial suffit pour établir qu’un espace topologique n’est pas connexe.

En effet, l’existence d’un tel ensemble démontre que l’espace peut être écrit comme la réunion de deux ouverts disjoints et non vides, \( \{ a, b \} \) et \( \{ c, d \} \). La condition de connexité topologique n’est donc pas vérifiée.

Exemple 2 : la droite réelle

Considérons l’ensemble des nombres réels \( \mathbb{R} \), muni de la topologie usuelle engendrée par les intervalles ouverts \( (a, b) \).

Dans cette topologie, les intervalles \( (a, b) \) sont des ensembles ouverts mais non fermés, tandis que les intervalles \( [a, b] \) sont fermés mais non ouverts.

Les seuls sous-ensembles de \( \mathbb{R} \) qui sont à la fois ouverts et fermés sont \( \mathbb{R} \) et \( \emptyset \).

Par conséquent, la droite réelle munie de la topologie usuelle est un espace connexe.

Exemple 3 : un sous-espace non connexe de \( \mathbb{R} \)

Considérons le sous-espace \( X = (0,1) \cup (2,3) \subset \mathbb{R} \), muni de la topologie induite par la topologie usuelle de \( \mathbb{R} \).

Dans ce cadre, les intervalles \( (0,1) \) et \( (2,3) \) sont à la fois ouverts et fermés dans \( X \), car le complémentaire de chacun dans \( X \) est exactement l’autre intervalle. Plus précisément :

• le complémentaire de \( (0,1) \) dans \( X \) est \( (2,3) \), qui est ouvert dans \( X \) ;
• le complémentaire de \( (2,3) \) dans \( X \) est \( (0,1) \), également ouvert dans \( X \).

Ces deux sous-ensembles sont donc clopen.

Comme il existe des sous-ensembles non triviaux qui sont simultanément ouverts et fermés, le sous-espace \( X \) est non connexe.

Autrement dit, \( X \) se compose de deux composantes connexes distinctes, \( (0,1) \) et \( (2,3) \), qui sont des ouverts disjoints et non vides. C’est précisément cette impossibilité de relier les points de l’un à ceux de l’autre par une continuité topologique qui caractérise la non-connexité.