Espaces connexes en topologie
Que veut-on dire quand on dit qu’un espace est connexe ?
En topologie, on dit qu’un espace $X$ est connexe lorsqu’il est impossible de le “découper” en deux parties ouvertes totalement séparées. Autrement dit, il n’existe pas deux ensembles ouverts non vides $U$ et $V$ tels que :
- $U \neq \emptyset$ et $V \neq \emptyset$ - les deux contiennent des points ;
- $U \cap V = \emptyset$ - ils n’ont aucun point en commun ;
- $U \cup V = X$ - ensemble, ils forment tout l’espace.
Si une telle paire existe, on dit que l’espace est disconnexe.
De manière intuitive, un espace est connexe lorsqu’il ne peut pas être “cassé” en deux régions ouvertes isolées l’une de l’autre. Si au contraire il peut l’être, il est disconnexe, et la paire $(U, V)$ qui le sépare s’appelle une séparation.
Remarque. C’est la définition formelle de la connexité topologique. Nous verrons plus loin qu’elle ne coïncide pas toujours avec la notion plus intuitive de connexité par chemins.
Un exemple simple pour comprendre
Imaginons un petit espace composé de trois points :
$$ X = \{a, b, c\} $$
Sur cet ensemble, on peut construire plusieurs topologies, c’est-à-dire différentes façons de définir quels sous-ensembles sont ouverts. Regardons deux cas particuliers :
- Topologie A
$$ \mathcal{T}_A = \{ \emptyset, X, \{a,b\}, \{b\}, \{b,c\} \} $$ - Topologie B
$$ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $$
Le but est de savoir laquelle de ces deux topologies rend l’espace connexe.
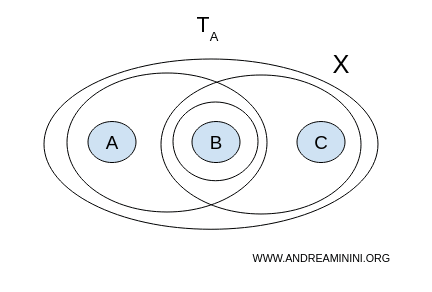
1) Le cas de la topologie A
Essayons de trouver deux ouverts non vides, disjoints et dont la réunion donne $X$ tout entier.
- $U = \{a,b\}, V = \{b,c\}$ → ils ne sont pas disjoints (ils partagent $b$) ;
- $U = \{a,b\}, V = \{b\}$ → idem ;
- $U = \{b\}, V = \{b,c\}$ → encore une intersection.
Aucune séparation n’est possible sans chevauchement. Donc, $X$ avec la topologie A est connexe.
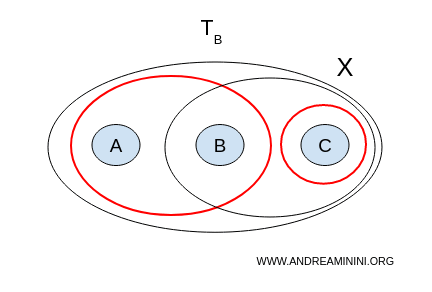
2) Le cas de la topologie B
Refaisons l’expérience avec : $ \mathcal{T}_B = \{ \emptyset, X, \{a,b\}, \{c\}, \{b,c\} \} $.
- $U = \{a,b\}, V = \{b,c\}$ → ils ne sont pas disjoints ;
- $U = \{a,b\}, V = \{c\}$ → cette fois, ils sont disjoints, non vides, et leur réunion couvre $X$.
Nous avons trouvé une séparation. L’espace $X$ muni de la topologie B est donc disconnexe.
Remarque. Ce petit exemple montre que la connexité ne dépend pas seulement des points de l’espace, mais de la topologie choisie. Avec les mêmes éléments, une topologie peut garder l’espace uni, tandis qu’une autre le sépare.
Un autre exemple : la droite réelle sans un point
Considérons maintenant l’espace :
$$ X = (-\infty, n) \cup (n, +\infty) $$
C’est la droite réelle privée d’un point :
$$ X = \mathbb{R} \setminus \{n\} $$
Posons : $ U = (-\infty, n) $ et $ V = (n, +\infty) $.
- Les deux ensembles sont ouverts dans la topologie usuelle de $\mathbb{R}$.
- Ils sont disjoints (aucun point en commun).
- Et ils sont tous deux non vides.
Leur réunion donne bien $X$, donc toutes les conditions d’une séparation sont réunies.
$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$
L’espace $ X = (-\infty, n) \cup (n, +\infty) $ est donc disconnexe, car il se divise naturellement en deux régions ouvertes séparées.
Remarque. Supprimer un seul point de la droite réelle suffit à “rompre” sa continuité : il reste deux intervalles, à gauche et à droite, qu’aucun chemin continu ne peut relier. L’espace est donc non seulement disconnexe, mais aussi non connexe par chemins.
Connexité topologique et connexité par chemins
Ces deux notions se ressemblent, mais elles ne sont pas équivalentes.
Un espace peut être connexe sans être connexe par chemins. Voici la différence :
- Connexité topologique
L’espace ne peut pas être décomposé en deux ouverts disjoints et non vides dont la réunion couvre tout l’espace. - Connexité par chemins
Tout couple de points peut être relié par un chemin continu à l’intérieur de l’espace. Si le chemin ne s’auto-intersecte pas, on parle alors de connexité par arcs.
En résumé, tout espace connexe par chemins est connexe, mais la réciproque n’est pas vraie : certains espaces connexes ne sont pas connexes par chemins.
Lorsqu’un chemin continu relie deux points, l’espace ne peut pas être séparé en deux régions isolées. Pourtant, certains espaces, bien que “indivisibles” topologiquement, ne permettent pas de tracer un chemin reliant certains points.
Exemple emblématique : la courbe du sinus du topologue :
$$ S = \{ (x, \sin(1/x)) \mid x > 0 \} \cup \{ (0, y) \mid -1 \le y \le 1 \} $$
Cette figure est connexe, car elle ne peut pas être séparée en deux ouverts disjoints. Mais elle n’est pas connexe par chemins : aucun chemin continu ne relie un point de la partie oscillante à un point du segment vertical.
En topologie, cela illustre une idée clé : “être connecté” ne signifie pas forcément “pouvoir passer d’un point à un autre par un chemin continu”.
Notes
Quelques compléments sur la notion d’espace connexe
- Théorème : caractérisation des espaces connexes par les ensembles ouverts et fermés (clopen)
Un espace topologique \( X \) est connexe lorsque les seuls sous-ensembles à la fois ouverts et fermés (clopen) sont l’espace tout entier \( X \) et l’ensemble vide \( \emptyset \). Ce critère constitue une méthode directe et élégante pour déterminer si un espace peut être séparé en sous-ensembles disjoints ou s’il forme un tout indivisible.
D’autres résultats et exemples approfondissent cette idée et montrent que la connexité est l’une des propriétés structurelles essentielles en topologie.