Connexité par intersection commune
Soient \( C_1, C_2, \dots, C_n \subset X \) des sous-ensembles connexes d'un espace topologique \( X \) tels que leur intersection soit non vide : \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Dans ce cas, leur union \( \bigcup_{i=1}^n C_i \) est elle aussi un ensemble connexe.
Autrement dit, dès que plusieurs ensembles connexes partagent au moins un point, leur réunion forme un tout qui reste connexe.
Ce résultat repose sur une idée simple mais fondamentale : l'existence d'un point commun empêche toute séparation de l'ensemble obtenu.
Remarque. La condition \( \bigcap_{i=1}^n C_i \neq \varnothing \) est suffisante pour garantir la connexité de l'union \( \bigcup_{i=1}^n C_i \), mais elle n'est pas nécessaire. Une union d'ensembles connexes peut rester connexe même en l'absence de point commun à tous. Cela se produit notamment lorsque les ensembles se recouvrent de manière progressive ou en chaîne.
Un exemple concret
Considérons les sous-ensembles suivants de \( \mathbb{R}^2 \) :
- \( C_1 \) : le segment horizontal reliant \( (-1,0) \) à \( (1,0) \)
- \( C_2 \) : le segment vertical reliant \( (0,-1) \) à \( (0,1) \)
- \( C_3 \) : le segment diagonal reliant \( (-1,-1) \) à \( (1,1) \)
Chacun de ces ensembles est connexe.
Ils partagent en outre un point commun, à savoir \( (0,0) \). En effet :
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
L'intersection commune n'est donc pas vide :
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
D'après le critère précédent, leur union est donc un ensemble connexe :
\[ C_1 \cup C_2 \cup C_3 \]
Les trois segments se rejoignent en un même point central, ce qui garantit la connexité de leur réunion.
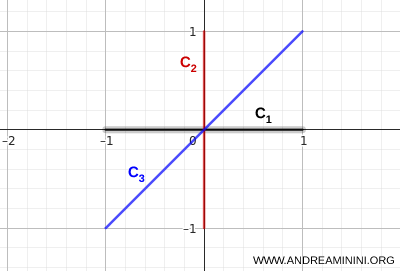
Depuis n'importe quel point de l'un des segments, on peut atteindre n'importe quel autre point en restant entièrement à l'intérieur de l'union.
Remarque. Il existe d'autres critères de connexité ne reposant pas sur l'existence d'un point commun à tous les ensembles. Par exemple, si les ensembles \( C_i \) sont connexes et se recoupent de manière enchaînée, c'est-à-dire si \( C_i \cap C_{i+1} \neq \varnothing \), alors leur union \( \bigcup_i C_i \) est connexe même si \( \bigcap_i C_i = \varnothing \). Cette condition n'est toutefois pas indispensable. L'union peut rester connexe même lorsque certaines paires consécutives sont disjointes, pourvu que d'autres ensembles assurent la liaison. Un exemple classique est celui de trois segments formant un triangle. Bien que leur intersection globale soit vide, \( \bigcap_i C_i = \varnothing \), leur union reste connexe.
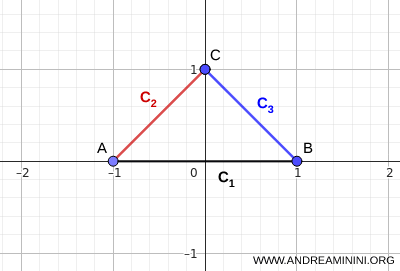
Cet exemple illustre clairement que la connexité peut résulter d'un enchaînement d'intersections locales.
Démonstration
Soit \( X \) un espace topologique et soit \( \{C_i\}_{i \in I} \) une famille de sous-ensembles connexes de \( X \) dont l'intersection est non vide :
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Supposons, par l'absurde, que l'union
\[ C = \bigcup_{i \in I} C_i \]
ne soit pas connexe.
Dans ce cas, il existe deux ouverts \( U \) et \( V \) qui forment une séparation de \( C \), c'est-à-dire :
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Puisque l'intersection des ensembles \( C_i \) est non vide, il existe un point
\[ x \in \bigcap_{i \in I} C_i \]
Ce point appartient donc à tous les ensembles \( C_i \), et en particulier à \( C \). Il appartient nécessairement à \( U \) ou à \( V \), mais pas aux deux, puisque ceux-ci forment une séparation de \( C \). Supposons, sans perte de généralité, que
\[ x \in U \quad \text{et} \quad x \notin V \]
Comme chaque ensemble \( C_i \) est inclus dans \( C \), on a :
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Les ensembles \( C_i \cap U \) et \( C_i \cap V \) sont ouverts dans la topologie induite sur \( C_i \), disjoints, et leur réunion reconstitue \( C_i \). Or chaque \( C_i \) est connexe, donc l'un de ces deux ensembles est nécessairement vide.
Il en résulte que chaque \( C_i \) est entièrement contenu soit dans \( U \), soit dans \( V \).
Comme \( x \in C_i \) et \( x \in U \), il est impossible que \( C_i \subset V \). On obtient donc :
\[ C_i \subset U \quad \text{pour tout } i \in I \]
Par conséquent, l'union \( C \) est elle-même contenue dans \( U \) :
\[ \bigcup_{i \in I} C_i \subset U \]
Ceci contredit l'hypothèse selon laquelle \( V \cap C \neq \varnothing \).
La contradiction montre que l'hypothèse initiale est fausse. On conclut donc que l'union \( \bigcup_{i \in I} C_i \) est un ensemble connexe.
Et ainsi de suite.