Espaces connexes par arcs
Un espace topologique S est connexe par arcs s'il existe un chemin continu reliant n'importe quels deux points A et B de cet espace, sans en sortir.
Imaginez une feuille de papier, sans tenir compte de ses bords.
Elle représente une aire continue et est considérée comme ouverte, excluant les frontières.
Sur cette feuille, il est possible de relier deux points quelconques A et B avec un stylo, sans jamais le lever de la surface.
En somme, le chemin ne quitte pas l'espace qui englobe les points A et B.
Un espace connexe par arcs est naturellement un espace connexe.
Cela semble intuitif : un espace disjoint serait divisé en plusieurs parties, rendant impossible la liaison continue entre deux points sans sortir de cet espace.
Cependant, l'inverse n'est pas systématiquement vrai. Tous les espaces connexes ne sont pas forcément connexes par arcs.
Prenons un cas qui peut paraître paradoxal mais qui est parfaitement plausible.
Considérez par exemple deux ensembles, Q et T :
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$
$$ T = \{ \ 0 \} $$
Le premier ensemble, Q, contient tous les points le long d'une onde sinusoïdale définie pour tous les nombres réels R sauf zéro, où la fonction n'est pas définie à cause d'une division par zéro - une opération indéfinie.
Le second ensemble, T, se compose uniquement du point zéro.
Les deux ensembles Q et T sont infiniment proches l'un de l'autre, comme le montre le graphique de la fonction continue sin(1/x).
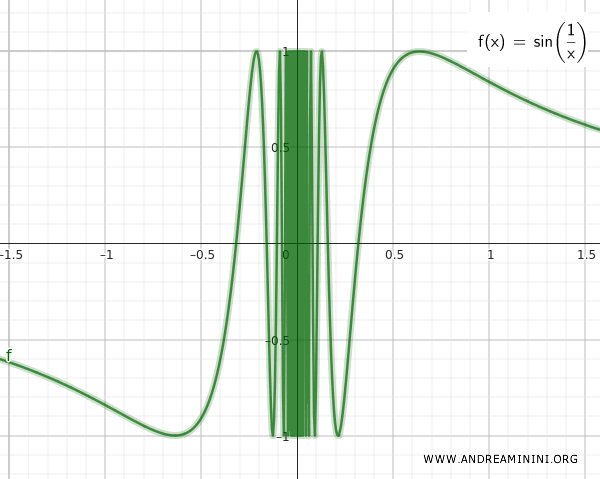
L'ensemble S est la réunion des ensembles Q et T.
$$ S = Q \cup T $$
L'ensemble S est connexe car, pour tout ε>0, il existe un voisinage autour de zéro (0-ε, 0+ε) qui inclut des points de l'ensemble Q.
Cela se produit parce que zéro est un point d'accumulation de la fonction sin(1/x).
Pourtant, S n'est pas connexe par arcs car il n'existe aucun arc qui puisse relier un point quelconque de Q à zéro (ensemble T).
Note : La situation serait différente avec la fonction f(x)=1/x, car dans ce cas, il est évident que les ensembles Q et T sont disjoints, et non pas infiniment proches.
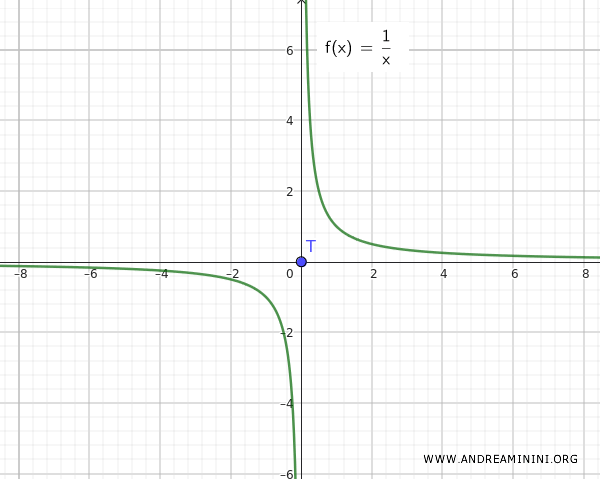
Cet exemple illustre que l'union d'un ensemble connexe Q={∀ x ∈ R-{0}, 1/x} et d'un point isolé T={0} ne crée pas nécessairement un ensemble connexe, à moins que ce point isolé (par exemple, zéro) serve aussi de point d'accumulation.
Et ainsi de suite.