Séparation d’un sous-ensemble par des ouverts

Soit $ A $ un sous-ensemble d’un espace topologique $ X $. Pour comprendre comment un ensemble peut être « découpé » en deux parties distinctes, on s’appuie sur deux ouverts du même espace, notés $ U $ et $ V $. On dit qu’ils réalisent une séparation de $ A $ lorsque trois conditions simples sont réunies :

Ils recouvrent entièrement $ A $ \[ A \subseteq U \cup V \]
Chacun d’eux contient au moins un point de $ A $ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Aucun point de $ A $ ne se trouve dans les deux ouverts à la fois \[ U \cap V \cap A = \varnothing \]

Autrement dit, ces conditions garantissent que $ A $ est « scindé » en deux zones non superposées, l’une entièrement dans $ U $ et l’autre entièrement dans $ V $. Aucun élément de $ A $ ne peut appartenir aux deux ouverts simultanément, ce qui correspond à la notion centrale de séparation en topologie.

Cette façon de procéder est l’une des plus directes pour déterminer, à l’aide des ouverts, quand un sous-ensemble peut réellement être considéré comme séparé.

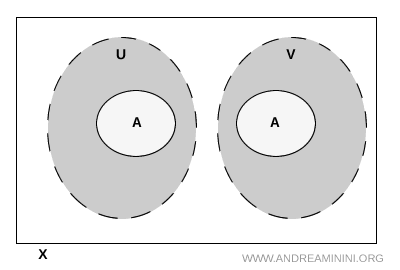
schéma illustrant la séparation d’un sous-ensemble par deux ouverts

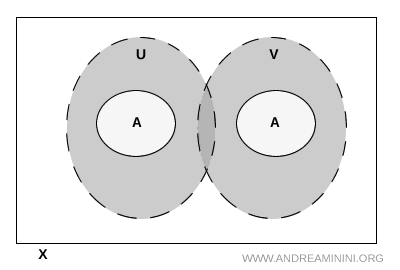
Nota. Il est possible que $ U $ et $ V $ s’intersectent en dehors de $ A $. Cela ne pose aucun problème, du moment que cette intersection ne contient pas de points de $ A $. C’est uniquement cette dernière condition qui compte pour la séparation.
schéma indiquant que deux ouverts peuvent s’intersecter hors de A sans affecter la séparation

Exemple concret

Pour voir comment la notion s’applique dans un cas simple, prenons l’espace $ X = \mathbb{R} $ muni de sa topologie usuelle. Considérons l’ensemble :

$$ A = [-2,-1] \cup [1,2] $$

Il se compose de deux intervalles fermés qui ne se touchent pas.

Choisissons ensuite les ouverts suivants :

$$ U = (-3,0) $$

$$ V = (0,3) $$

Voici leur représentation sur la droite réelle :

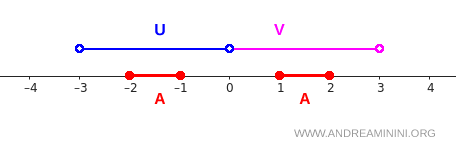
droite réelle illustrant U, V et les deux composantes de A

L’intervalle $ [-2,-1] $ se trouve entièrement dans $ U $, tandis que $ [1,2] $ est entièrement dans $ V $. La vérification des conditions suit immédiatement :

1. L’ensemble $ A $ est bien inclus dans l’union des deux ouverts :

$$ A \subseteq U \cup V $$

2. Chacun d’eux rencontre $ A $ :

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

3. Aucun point de $ A $ n’appartient aux deux ouverts simultanément :

$$ U \cap V \cap A = \varnothing $$

On conclut donc que $ U $ et $ V $ séparent effectivement le sous-ensemble $ A $ dans l’espace $ X $. La structure de $ A $, composée de deux blocs bien distincts, permet ici de visualiser clairement la notion abstraite de séparation.