Espaces simplement connexes en topologie

Un espace topologique est qualifié de simplement connexe lorsqu'il est possible de réduire continuellement chaque chemin fermé de cet espace en un unique point.

Autrement dit, un espace est simplement connexe si l'on peut contracter n'importe quelle boucle jusqu'à un point, sans sortir de cet espace.

Cela indique que l'espace constitue un bloc cohérent (espace connexe) exempt de tout « trou » interne.

Note : de ce fait, un espace simplement connexe est également un espace connexe. Cependant, la réciproque n'est pas systématique : tous les espaces connexes ne sont pas simplement connexes.

Un exemple concret

Considérons une sphère, par exemple, qui représente un espace topologique simplement connexe car toute courbe fermée en son sein peut être contractée en un point unique.

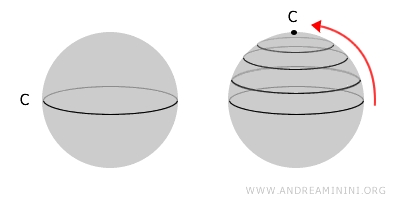
À l'opposé, un tore, ou « donut », n'est pas simplement connexe à cause de son trou central, empêchant certaines boucles de se réduire à un point.

Ceci démontre aussi que le fait d'être connexe ne signifie pas nécessairement une simple connectivité.

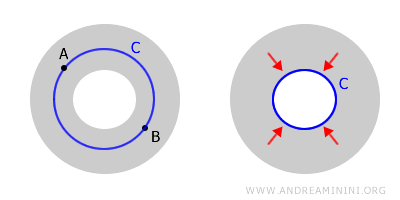
Le « donut » est un espace connexe car il est possible de relier deux points quelconques, A et B, par un chemin qui reste à l'intérieur de l'espace.

Cependant, le « donut » n'est pas simplement connexe car on ne peut pas contracter toutes ses courbes fermées en des points.

Dans ces situations, où un espace est connexe mais pas simplement connexe, on parle d'espace multiplement connexe. Des exemples incluent la région annulaire ou l'espace toroïdal.

Par conséquent, la simple connectivité est une exigence plus stricte que la connectivité par arcs.