Frontière d’un ensemble

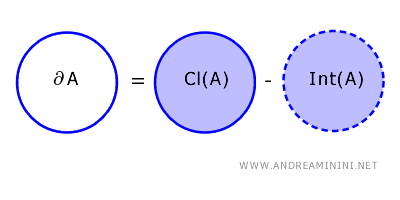
La frontière d’une partie $ A $ d’un espace topologique $ X $ est l’ensemble des points qui appartiennent à l’adhérence de $ A $ sans appartenir à son intérieur : \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Ici, $ \text{Cl}(A) $ désigne l’adhérence de $ A $, qui comprend les points de $ A $ ainsi que ses points limites.

De même, $ \text{Int}(A) $ correspond à l’intérieur de $ A $, c’est-à-dire l’ensemble des points admettant un voisinage entièrement contenu dans $ A $.

example of boundary of a set

Il est important de souligner que la notion de frontière dépend de la topologie considérée, et ne constitue donc pas une propriété intrinsèque de l’ensemble.

En conséquence, la frontière d’un même ensemble peut différer selon la topologie choisie.

Autrement dit, la frontière d’un ensemble $ A $ est constituée des points qui sont « proches » à la fois de $ A $ et de son complémentaire $ X \setminus A $.

Un exemple concret
Théorème de la frontière
Remarques

Un exemple concret

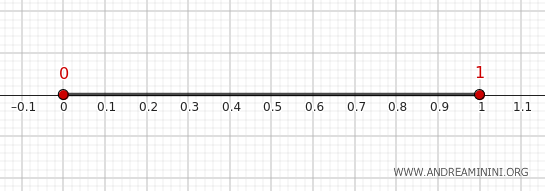
Considérons l’ensemble $ A = (0, 1) $, vu comme sous-ensemble de la droite réelle $ \mathbb{R} $ munie de sa topologie usuelle.

Déterminons sa frontière en procédant par étapes.

1] Adhérence de A

L’adhérence de $ A $, notée $ \text{Cl}(A) $, contient tous les points de $ A $ ainsi que ses points d’accumulation.

Dans le cas de $ A = (0, 1) $, l’adhérence est l’intervalle fermé $[0, 1]$, car les bornes 0 et 1 sont elles-mêmes limites pour $ A $, tout comme les points à l’intérieur.

$$ \text{Cl}(A) = [0, 1] $$

2] Intérieur de A

L’intérieur de $ A $, noté $ \text{Int}(A) $, est formé des points qui possèdent un voisinage entièrement inclus dans $ A $.

Comme $ A = (0, 1) $ est déjà un intervalle ouvert, son intérieur est égal à lui-même :

$$ \text{Int}(A) = (0, 1) $$

3] Frontière de A

La frontière de $ A $, soit $ \partial A $, s’obtient en retranchant son intérieur à son adhérence :

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

En remplaçant par les expressions obtenues :

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Ainsi, dans la topologie usuelle de $ \mathbb{R} $, la frontière de l’ensemble $ A = (0,1) $ est constituée des points $\{0, 1\}$.

Ces deux points se situent « au bord » de l’ensemble, car tout voisinage de chacun d’eux contient à la fois des éléments de $ A $ et de $ X \setminus A $.

example of set boundary

Théorème de la frontière

Un point $ x \in X $ appartient à la frontière $ \partial A $ d’un sous-ensemble $ A $ si, et seulement si, tout voisinage de $ x $ rencontre à la fois $ A $ et son complémentaire $ X - A $.

Ce théorème fournit un critère opérationnel : pour savoir si un point $ x $ appartient à la frontière de $ A $, il suffit de vérifier que tout voisinage de $ x $ intersecte simultanément $ A $ et $ X - A $.

Exemple

Reprenons $ A = (0, 1) $ dans $ \mathbb{R} $, muni de la topologie standard.

On a alors :

$$ \text{Cl}(A) = [0, 1] \quad \text{et} \quad \text{Int}(A) = (0, 1) $$

Donc la frontière est :

$$ \partial A = \{0, 1\} $$

Vérifions que ces points respectent bien le critère du théorème.

1] Vérification pour le point 0

Considérons un voisinage de 0, par exemple $ (0 - \epsilon, 0 + \epsilon) $ avec $ \epsilon > 0 $.

Ce voisinage intersecte $ A $, puisqu’il contient des points de $ (0, 1) $, et intersecte aussi $ X - A $, car il contient des points inférieurs ou égaux à 0.

Par conséquent, $ 0 \in \partial A $.

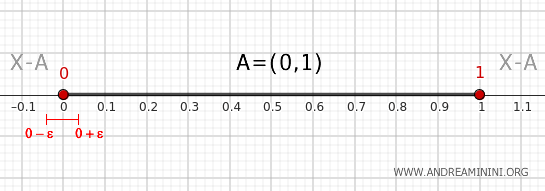
Neighborhood of point 0

2] Vérification pour le point 1

Considérons maintenant un voisinage de 1, par exemple $ (1 - \epsilon, 1 + \epsilon) $.

Ce voisinage coupe également $ A $ (puisqu’il contient des points de $ (0,1) $) et $ X - A $, en incluant des points supérieurs ou égaux à 1.

Ainsi, $ 1 \in \partial A $.

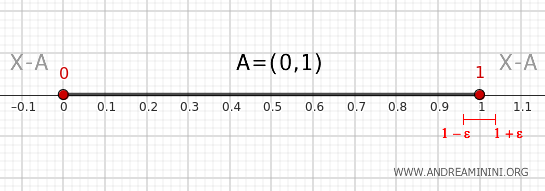
Neighborhood of point 1

3] Vérification pour un point intérieur

Choisissons un point quelconque dans l’intervalle $ (0,1) $, par exemple 0,5.

Tout voisinage de 0,5 est entièrement contenu dans $ A $, et ne peut donc pas rencontrer $ X - A $.

On en conclut que $ 0.5 \notin \partial A $.

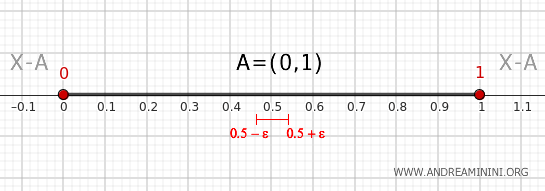
Neighborhood of 0.5

En résumé, le théorème confirme que les points 0 et 1 appartiennent bien à la frontière de $ A = (0, 1) $, tandis qu’un point comme 0,5 n’en fait pas partie. La frontière est donc $\{0, 1\}$.

Remarques

Quelques propriétés importantes concernant les frontières en topologie :

La frontière $ \partial A $ est incluse dans $ A $ si et seulement si $ A $ est fermé :
\[ \partial A \subseteq A \Leftrightarrow A \text{ est fermé} \]
La frontière $ \partial A $ et $ A $ sont disjoints si et seulement si $ A $ est ouvert :
Autrement dit, $ A $ est ouvert ⇔ aucun de ses points ne se trouve sur sa frontière.
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ est ouvert} \]
La frontière $ \partial A $ est vide si et seulement si $ A $ est à la fois ouvert et fermé (clopen) :
\[ \partial A = \emptyset \Leftrightarrow A \text{ est clopen} \]
La frontière $ \partial A $ est l’intersection de l’adhérence de $ A $ avec celle de son complémentaire $ X - A $ :
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
La frontière $ \partial A $ est toujours un ensemble fermé

L’intersection de deux fermés est elle-même fermée. Puisque $ \partial A $ est défini par $\text{Cl}(A) \cap \text{Cl}(X - A)$, on peut en conclure que $ \partial A $ est toujours fermé.
La frontière et l’intérieur d’un ensemble sont toujours disjoints :
\[ \partial A \cap \text{Int}(A) = \emptyset \]
L’union de l’intérieur et de la frontière est égale à l’adhérence de l’ensemble :
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

Et ainsi de suite.