Théorème de la frontière d’un ensemble
Un point \( x \) appartient à la frontière d’un ensemble \( A \) si, pour tout voisinage de \( x \), on rencontre à la fois des points de \( A \) et des points de son complémentaire \( X - A \).
Autrement dit, si aucun voisinage de \( x \) n’est entièrement contenu dans \( A \), ni entièrement dans \( X - A \), alors \( x \) est un point frontière de \( A \).
Un exemple illustratif
Considérons un exemple concret permettant de mieux visualiser cette notion.
Soit l’ensemble \( A = (0, 1) \) dans la droite réelle \( \mathbb{R} \).
Les points 0 et 1 appartiennent à la frontière de \( A \), car tout voisinage de ces points contient nécessairement des éléments situés à l’intérieur de l’intervalle \( (0, 1) \) ainsi que d’autres à l’extérieur.
- Point 1
Tout voisinage de la forme \( (1 - \epsilon, 1 + \epsilon) \), avec ε arbitrairement petit, contient une partie \( (1 - \epsilon, 1) \) incluse dans \( A \), et une autre \( (1, 1 + \epsilon) \) située hors de \( A \). Le point 1 est donc un point frontière de \( A \).
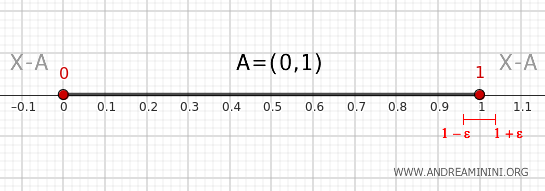
- Point 0
De façon analogue, tout voisinage \( (0 - \epsilon, 0 + \epsilon) \) contient une portion \( (0, 0 + \epsilon) \) incluse dans \( A \), ainsi qu’une portion \( (0 - \epsilon, 0) \) située dans le complémentaire. Le point 0 appartient donc lui aussi à la frontière de \( A \).
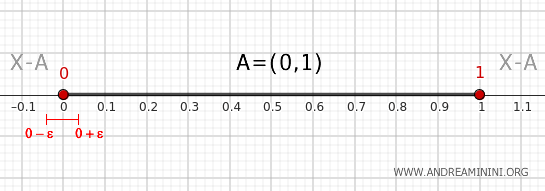
- Point intérieur à l’intervalle (0, 1)
Tout point \( x \) strictement compris entre 0 et 1 possède un voisinage \( (x - \epsilon, x + \epsilon) \), avec ε > 0, entièrement contenu dans \( A \). Ce voisinage n’intersecte donc pas le complémentaire, et ces points ne sont pas sur la frontière.
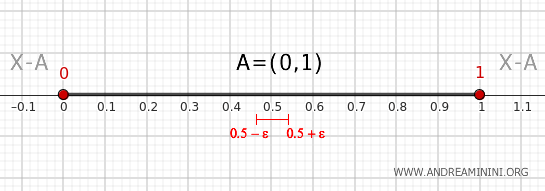
- Point extérieur à l’intervalle (0, 1)
Tout point strictement extérieur à l’intervalle \( (0, 1) \), à l’exception des bornes 0 et 1, admet un voisinage \( (x - \epsilon, x + \epsilon) \) entièrement contenu dans \( X - A \), sans aucune intersection avec \( A \). Ces points ne font donc pas partie de la frontière.
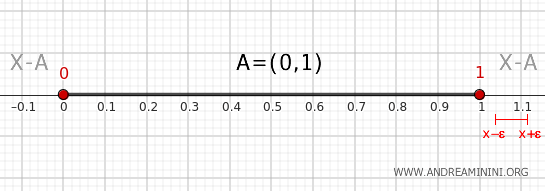
On en déduit que les seuls points frontière de \( A \) sont 0 et 1 :
$$ \partial A = \{0,1 \} $$
En résumé, un point \( x \) appartient à la frontière de \( A \) si l’on ne peut trouver aucun voisinage de \( x \) contenu intégralement dans \( A \), ni dans son complémentaire. Ce critère permet d’identifier précisément les points frontières.
La démonstration
Pour établir ce théorème, on considère deux implications :
1] Supposons que \( x \in \partial A \)
Par définition, cela signifie que :
$$ x \in \text{Cl}(A) \quad \text{et} \quad x \notin \text{Int}(A) $$
Le fait que \( x \in \text{Cl}(A) \) implique que tout voisinage de \( x \) rencontre \( A \).
Le fait que \( x \notin \text{Int}(A) \) signifie qu’aucun voisinage de \( x \) n’est entièrement inclus dans \( A \), donc chacun d’eux contient nécessairement des points de \( X - A \).
Ainsi, tout voisinage de \( x \) intersecte simultanément \( A \) et \( X - A \).
2] Supposons que tout voisinage de \( x \) coupe à la fois \( A \) et \( X - A \)
Alors, par définition, \( x \in \text{Cl}(A) \) et \( x \in \text{Cl}(X - A) \).
Or, comme \( \text{Cl}(X - A) = X - \text{Int}(A) \), il s’ensuit que \( x \notin \text{Int}(A) \).
Par conséquent, \( x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A \).
La réciproque est donc démontrée : \( x \) est bien un point frontière de \( A \).