Espace topologique normal

Un espace topologique $ X $ est dit normal s’il vérifie les deux conditions suivantes :

Les singletons sont fermés
Autrement dit, pour tout point $ x \in X $, l’ensemble $\{x\}$ est fermé dans la topologie considérée.
Tout couple d’ensembles fermés disjoints peut être séparé par des ouverts disjoints
Si $ A $ et $ B $ sont deux ensembles fermés tels que $ A \cap B = \emptyset $, alors il existe deux ouverts $ U $ et $ V $ tels que :
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $

La normalité signifie qu’il est toujours possible, dans un tel espace, de "loger" deux ensembles fermés disjoints dans des ouverts séparés qui ne se recouvrent pas.

Autrement dit, cette propriété garantit que, dès que deux ensembles fermés sont disjoints, on peut les inclure chacun dans un ouvert qui ne touche pas l’autre.

Il s’agit d’une condition essentielle dans la construction de fonctions continues capables de distinguer des points d’un espace.

Exemple concret
Remarques supplémentaires

Exemple concret

Considérons l’espace topologique $ X = \mathbb{R} $, muni de la topologie usuelle générée par les intervalles ouverts $ (a, b) $.

On prend deux ensembles fermés et disjoints de $ \mathbb{R} $ :

$ A = \{0\} $, un singleton.
$ B = [2, 3] $, un intervalle fermé.

Ces deux ensembles sont fermés dans la topologie usuelle de $ \mathbb{R} $, et comme ils n’ont aucun point en commun, ils sont disjoints.

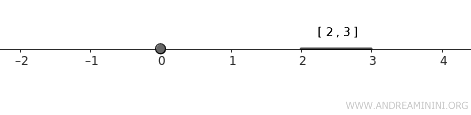
example

Remarque. L’ensemble $ A $ se réduit à un seul point, ce qui en fait un fermé. L’intervalle $ B $, quant à lui, est fermé par définition.

Nous allons maintenant construire deux ouverts disjoints qui contiennent respectivement $ A $ et $ B $.

Un bon choix pour $ A $ est l’ouvert $ U = (-1, 1) $, qui contient $ \{0\} $.

$$ A \subset U = (-1,1) $$

Pour $ B = [2,3] $, on peut prendre $ V = (1, 4) $, qui l’englobe entièrement.

$$ B \subset V = (1,4) $$

Les ouverts $ U $ et $ V $ sont disjoints, c’est-à-dire que $ U \cap V = \emptyset $, ce qui confirme la condition de normalité.

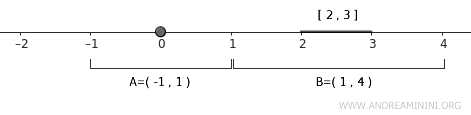
example

Le même raisonnement s’applique à tout couple d’ensembles fermés disjoints : on peut toujours trouver deux ouverts disjoints les englobant.

On en conclut que la droite réelle $ X = \mathbb{R} $, munie de la topologie usuelle, est un espace normal.

Remarques supplémentaires

Quelques faits essentiels à propos des espaces normaux :

La droite réelle $ \mathbb{R} $ munie de la topologie usuelle est un espace normal
Elle satisfait non seulement la condition de régularité (qui permet de séparer un point d’un fermé à l’aide d’ouverts disjoints), mais aussi la condition plus forte de normalité.
Tout espace métrique est normal
Un espace muni d’une distance (métrique) entre ses points est nécessairement normal.
Tout espace normal est aussi régulier
La normalité implique la régularité, mais la réciproque n’est pas toujours vraie.

Et ainsi de suite.