Espace de Hausdorff
Un espace de Hausdorff est un espace topologique dans lequel tout couple de points distincts peut être séparé par des ouverts disjoints. Autrement dit, chaque point peut être distingué sans ambiguïté des autres au moyen de son propre voisinage ouvert.
De manière plus intuitive, cela signifie que pour tout \( x \ne y \), il existe des ouverts \( U \) et \( V \) tels que \( x \in U \), \( y \in V \) et \( U \cap V = \emptyset \).
Cette propriété formalise la notion de séparation conforme à notre intuition issue de la géométrie euclidienne : les points peuvent toujours être "tenus à distance" par des voisinages disjoints.
Les espaces de Hausdorff occupent une place centrale en analyse et en géométrie, notamment parce qu’ils permettent une théorie robuste de la convergence des suites et garantissent l’unicité des limites.
Un résultat classique est que, dans tout espace de Hausdorff, les singletons sont des ensembles fermés.
En effet, le complément d’un point est toujours un ouvert, ce qui implique que le point lui-même est fermé.
Exemples concrets
Exemple 1
Considérons la topologie usuelle sur la droite réelle \(\mathbb{R}\), fondée sur les intervalles ouverts.

Dans cette topologie, un singleton \( \{x\} \) n’est pas un ouvert.
Explication : Un ensemble est ouvert s’il contient un intervalle ouvert autour de chacun de ses points. Or, un singleton est dépourvu d’extension : il ne peut pas contenir de voisinage autour de \( x \) sans inclure d’autres points. Ainsi, \( \{x\} \) n’est pas ouvert dans la topologie usuelle.
En revanche, le complémentaire \( \mathbb{R} \setminus \{x\} \) est un ouvert.

Il en résulte que \( \{x\} \) est fermé, puisque son complément est ouvert.
De plus, \(\mathbb{R}\), muni de sa topologie usuelle, est un espace de Hausdorff : pour tout couple \( a \ne b \), on peut trouver des ouverts disjoints les contenant respectivement.
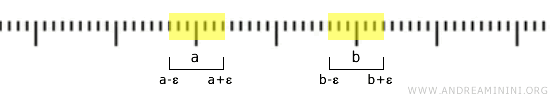
Par exemple, si \( a < b \), on peut choisir \( \varepsilon > 0 \) tel que \( a + \varepsilon < b - \varepsilon \), et prendre les intervalles ouverts \( (a - \varepsilon, a + \varepsilon) \) et \( (b - \varepsilon, b + \varepsilon) \), qui sont alors disjoints.
Ce type d’argument confirme que \(\mathbb{R}\), avec sa topologie standard, est bien un espace de Hausdorff.
Exemple 2
Considérons l’espace fini \( X = \{1, 2, 3\} \) muni de la topologie discrète.
Dans cette topologie, chaque singleton est un ouvert par définition.
Tous les sous-ensembles de \( X \) sont donc ouverts :
- le vide \( \emptyset \)
- les singletons \( \{1\}, \{2\}, \{3\} \)
- les paires \( \{1, 2\}, \{1, 3\}, \{2, 3\} \)
- l’ensemble total \( \{1, 2, 3\} \)
Il y a exactement \( 2^3 = 8 \) ouverts, correspondant à tous les sous-ensembles de \( X \).
Dans ce cadre, \( X \) est automatiquement un espace de Hausdorff.
Pour tout couple \( x \ne y \), on peut prendre les ouverts \( U = \{x\} \) et \( V = \{y\} \), qui sont disjoints et contiennent chacun leur point respectif.
Par exemple, si \( x = 1 \) et \( y = 2 \) :
$$ \{1\} \cap \{2\} = \emptyset $$
On vérifie donc que chaque paire de points peut être séparée par des ouverts disjoints.
Dans la topologie discrète, les singletons sont-ils ouverts ou fermés ?
La question peut paraître déroutante au début. Si la topologie discrète est de Hausdorff, les singletons doivent être fermés. Mais par définition, ils sont également ouverts. Comment cela est-il possible ?
La réponse est simple : en topologie, un ensemble peut être à la fois ouvert et fermé. On parle alors d’un ensemble clopen. Ici, “fermé” ne signifie pas “non ouvert”.
Dans la topologie discrète, chaque singleton \( \{x\} \) est fermé car son complémentaire est un sous-ensemble de \( X \), donc un ouvert. Et comme tous les sous-ensembles sont ouverts, leurs complémentaires le sont aussi.
Par exemple, si \( X = \{1, 2, 3\} \) et que l’on considère \( \{1\} \), c’est un ouvert par définition. Son complémentaire \( \{2, 3\} \) est également un ouvert, donc \( \{1\} \) est aussi fermé.
En somme, tout singleton \( \{x\} \) dans la topologie discrète est à la fois ouvert et fermé.
- Ouvert
Chaque point est un ouvert car tous les sous-ensembles sont ouverts. - Fermé
Le complémentaire \( X \setminus \{x\} \) est un sous-ensemble ouvert, ce qui rend \( \{x\} \) fermé.
Autrement dit, dans la topologie discrète, les singletons sont simultanément ouverts et fermés, car leurs complémentaires le sont aussi.
La principale différence entre la topologie discrète et la topologie usuelle est que, dans cette dernière, seuls certains sous-ensembles satisfont aux conditions d’ouverture. Tous ne sont pas nécessairement ouverts.
Observaciones
A continuación se presentan algunas propiedades fundamentales y consecuencias clave asociadas a los espacios de Hausdorff:
- En un espacio de Hausdorff, toda sucesión convergente admite un único límite
En cualquier espacio de Hausdorff \( X \), una sucesión que converge no puede tener más de un punto de acumulación. Es decir, si una sucesión converge, su límite es necesariamente único. Si existieran dos límites distintos, estos podrían separarse mediante entornos abiertos disjuntos, lo que llevaría a una contradicción con la definición de convergencia.
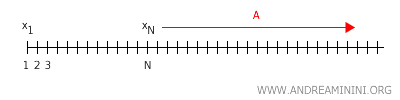
Demostración: Supongamos que \( X \) es un espacio de Hausdorff (por ejemplo, la recta real \( \mathbb{R} \)). Consideremos una sucesión \( x_1, x_2, x_3, \dots \) que converge simultáneamente a dos puntos distintos \( x \) e \( y \). Por definición de convergencia en un espacio topológico, esto significa que para todo entorno abierto \( U \) de \( x \), existe un entero \( N \) tal que para todo \( n > N \), se cumple \( x_n \in U \).
De forma análoga, para todo entorno abierto \( V \) de \( y \), existe \( M \in \mathbb{N} \) tal que \( x_n \in V \) para todo \( n > M \).
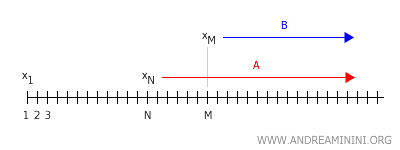
Sin embargo, si \( x \ne y \), la propiedad de Hausdorff garantiza la existencia de entornos abiertos disjuntos \( U \) y \( V \) que contienen respectivamente a \( x \) e \( y \). Por tanto, los términos de la sucesión tendrían que pertenecer simultáneamente a \( U \) y a \( V \) para valores suficientemente grandes de \( n \), lo que implicaría que \( U \cap V \ne \emptyset \), contradiciendo la disjunción entre ambos entornos.
Concluimos así que en un espacio de Hausdorff, ninguna sucesión puede converger a más de un punto. El límite, si existe, es único.