Espaces réguliers en topologie

En topologie, un espace régulier satisfait à une propriété de séparation plus forte que celle des espaces de Hausdorff.

Lorsqu’un espace est régulier et possède une base dénombrable, le théorème d’Urysohn garantit qu’il est métrisable.

Quelle est la différence avec les espaces de Hausdorff ?

Les espaces réguliers assurent qu’un point et un ensemble fermé disjoint peuvent être séparés par des ouverts distincts. Cette exigence est plus forte que celle des espaces de Hausdorff, où l’on demande uniquement que deux points distincts puissent être séparés par des ouverts disjoints.

Remarque. Un espace régulier n’est pas nécessairement un espace normal. Un espace normal impose une condition encore plus stricte : tout couple d’ensembles fermés disjoints doit pouvoir être séparé par des ouverts disjoints. Ainsi, tout espace normal est forcément régulier, mais l’inverse n’est pas toujours vrai.  

Il convient également de souligner que la régularité n’est qu’un type parmi d’autres de propriétés de séparation. Un espace topologique peut être régulier sans être de Hausdorff, ou être de Hausdorff sans être régulier. Il existe même des exemples d’espaces réguliers non hausdorffiens, et inversement.

Un exemple concret

Un exemple classique d’espace régulier est la droite réelle \( \mathbb{R} \), munie de sa topologie usuelle.

Considérons un point \( x \in \mathbb{R} \) et un ensemble fermé \( C \) qui ne contient pas \( x \).

Par exemple, prenons \( x = 2 \) et l’ensemble fermé suivant :

\[ C = (-\infty, 0] \cup [5, \infty) \]

Il est clair que \( x = 2 \notin C \), et que \( C \) est bien fermé pour la topologie standard.

Nous cherchons maintenant deux ouverts qui permettent de séparer \( x \) de \( C \).

Le complémentaire de \( C \) est un ouvert, et l’on peut y trouver un intervalle ouvert contenant \( x \).

Par exemple, l’intervalle \( (0, 5) \) contient le point \( x = 2 \).

\[ (a, b) = (0, 5) \]

Choisissons deux réels \( c \) et \( d \) tels que :

\[ 0 < c < 2 < d < 5 \]

Par exemple, \( c = 1 \) et \( d = 3 \) conviennent.

Définissons alors deux ouverts :

• \( U = (c, d) = (1, 3) \), qui contient le point \( x = 2 \).
• \( V = (-\infty, c) \cup (d, \infty) = (-\infty, 1) \cup (3, \infty) \), qui contient l’ensemble \( C \).

Ces deux ensembles sont disjoints, c’est-à-dire \( U \cap V = \emptyset \), et satisfont donc à la condition de régularité.

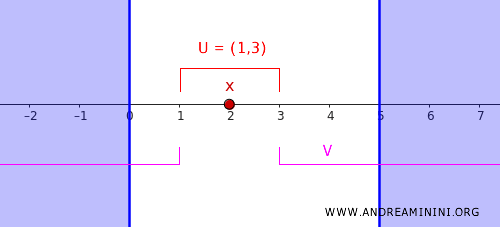
En résumé, nous avons réussi à séparer le point \( x = 2 \) de l’ensemble fermé \( C \) au moyen de deux ouverts disjoints \( U \) et \( V \), ce qui démontre que la droite réelle munie de la topologie usuelle est un espace régulier.

Notes

Quelques clés pour mieux comprendre les espaces réguliers

• Les axiomes de séparation
  En topologie, des notions comme Hausdorff et régulier font partie d'un ensemble de règles appelé les axiomes de séparation. Ces principes permettent de savoir jusqu'où un espace peut aller pour distinguer clairement ses points et ses sous-ensembles grâce à des voisinages ouverts qui ne se recoupent pas. Les connaître, c'est mieux comprendre le « pouvoir de distinction » d'une topologie : à quel point elle sait différencier les éléments d'un espace.

  Remarque. De façon intuitive, un espace est Hausdorff si l'on peut entourer deux points distincts par des ensembles ouverts qui ne se touchent pas. Il est régulier si l'on peut aussi séparer un point d'un ensemble fermé qui ne le contient pas, selon la même idée. Ces propriétés révèlent la capacité d'un espace à distinguer ses éléments avec précision - une sorte de « résolution topologique » comparable à celle d'une image : plus elle est élevée, plus les détails sont nets.

Et ainsi de suite.