Topologie Quotient

Soient $X$ un espace topologique et $A$ un ensemble qui n’est pas nécessairement un sous-ensemble de $X$. Supposons qu’il existe une application surjective $p : X \rightarrow A$. Un sous-ensemble $U$ de $A$ est dit ouvert si, et seulement si, $p^{-1}(U)$ est ouvert dans $X$.

Autrement dit, un ensemble $U$ de $A$ est ouvert dans la topologie quotient si, et seulement si, sa préimage $p^{-1}(U)$ - c’est-à-dire l’ensemble des points de $X$ envoyés dans $U$ par $p$ - est un ouvert de $X$.

illustration de topologie quotient

Ce principe permet de doter $A$ d’une nouvelle topologie, appelée topologie quotient, obtenue à partir de la topologie de $X$ via l’application $p$.

L’ensemble $A$ est alors appelé espace quotient et la fonction $p$, application quotient.

L’ensemble des ouverts de $A$ est souvent désigné comme la "topologie quotient induite par $p$".

En résumé, dans la topologie quotient, un ensemble est ouvert dès lors que sa préimage dans l’espace initial est ouverte.

Il est important de lever une confusion fréquente :

La préimage d’un ouvert de l’espace quotient $A$ est toujours un ouvert de $X$, mais la réciproque n’est pas nécessairement vraie.
L’image directe d’un ouvert de $X$ n’est pas forcément un ouvert de $A$, car l’application $p$ peut en modifier la structure.

En définitive, un espace quotient est un espace topologique construit à partir d’un autre en identifiant - ou “recollant” - certains de ses points selon une relation d’équivalence.

De façon intuitive, un espace quotient résulte de la “fusion” de certains points d’un espace, suivant une règle précise, afin d’en étudier ensuite les propriétés topologiques.

Pourquoi la topologie quotient est-elle utile ? Elle permet d’examiner les propriétés d’un espace $A$, souvent plus complexe, en s’appuyant sur les connaissances que l’on possède de $X$, généralement plus simple à manipuler.

Explication
Un exemple concret
Propriétés de la topologie quotient

Explication

La notion de "topologie quotient" peut sembler abstraite au premier abord, mais on peut en saisir l’intuition grâce à des exemples concrets.

La topologie quotient fournit un cadre pour transformer une figure en recollant entre elles certaines de ses arêtes ou de ses faces.

Imagine par exemple que tu disposes d’une feuille de papier carrée. Si tu colles deux côtés opposés, tu obtiens un cylindre.

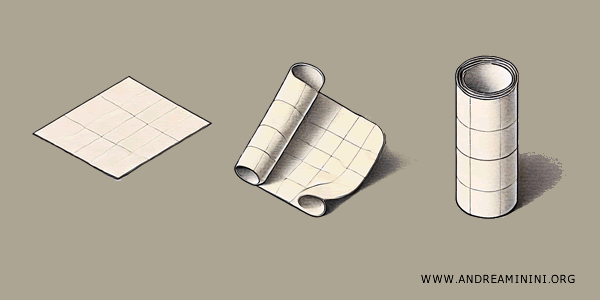
pliage d'une feuille pour former un cylindre

Si tu joins ensuite les bords circulaires du cylindre, tu obtiens une forme en anneau : un tore.

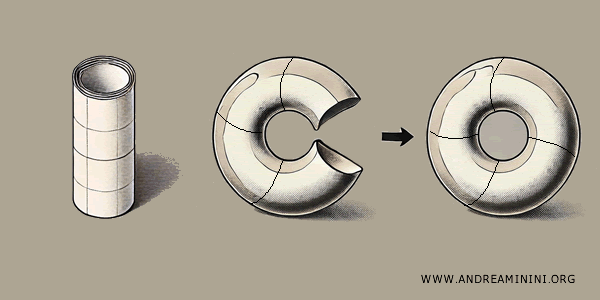
exemple de tore obtenu à partir d’un cylindre

Dans ce processus, le carré est d’abord transformé en cylindre, puis en tore, en recollant ses bords de façon appropriée.

De manière analogue, la topologie quotient permet de construire de nouveaux espaces topologiques à partir d’espaces plus simples, en identifiant certaines de leurs parties.

Cette approche est essentielle en mathématiques pour étudier de façon abstraite les propriétés globales des surfaces et des espaces.

Un exemple concret

Considérons l’espace topologique $ X = [0, 1] $, muni de la topologie usuelle, où les ouverts sont des intervalles ouverts ou des unions d’intervalles ouverts.

Dans cet espace, on a :

Les ensembles $X$ et $ \emptyset $ sont ouverts par définition.
Tout intervalle ouvert $ (a,b) $ avec $ 0 \leq a < b \leq 1 $ est un ouvert de $X$.

On peut représenter $X$ comme un segment de droite reliant les points $0$ et $1$.

représentation graphique du segment [0,1]

Construisons maintenant un espace quotient en identifiant les extrémités $0$ et $1$ de l’intervalle $[0, 1]$, autrement dit en les considérant comme un seul et même point.

On définit une application $ p : [0, 1] \rightarrow A $ de la façon suivante :

$$ p(x) = \begin{cases} p(0) & \text{si } x = 0 \text{ ou } x = 1 \\ \\ x & \text{si } 0 < x < 1 \end{cases} $$

L’espace quotient $A$ ainsi obtenu peut être visualisé comme un cercle dans lequel $0$ et $1$ ont été identifiés.

formation d’un cercle par topologie quotient

Autrement dit, nous avons “courbé” le segment pour en relier les extrémités et obtenir une figure fermée.

Dans ce nouvel espace $A$, le point $P = \{0,1\}$ représente l’image commune des deux extrémités sous l’application $p$.

Pour définir la topologie sur $A$, il faut déterminer quels sous-ensembles seront considérés comme ouverts.

Par définition, un ensemble $U \subseteq A$ est ouvert si sa préimage $p^{-1}(U)$ est un ouvert de $[0,1]$.

Voyons deux situations typiques :

Intervalle $ U = (a,b) $ ne contenant pas $P$
Sa préimage dans $X$ est l’intervalle ouvert $ (a,b) $, donc $U$ est ouvert dans $A$.
Intervalle $ U = (a,b) $ contenant $P = \{0,1\}$
Sa préimage dans $X$ est l’union des deux intervalles $ [0,a) \cup (b,1] $, chacun ouvert dans $X$. Ainsi, $U$ est un ouvert de $A$.

Nous avons ainsi construit un nouvel espace topologique $A$ - un cercle - à partir de l’intervalle $[0,1]$.

C’est un exemple classique de la manière dont la topologie quotient permet de transformer un espace élémentaire en un espace topologiquement plus riche.

Exemple 2

Dans ce second exemple de topologie quotient, nous cherchons à « enrouler » la droite réelle autour d’un cercle.

Considérons la droite réelle $ \mathbb{R} $, qui s’étend indéfiniment dans les deux directions.

L’idée consiste à « replier » cette droite sur un cercle, en identifiant chaque nombre réel à sa partie fractionnaire.

Pour cela, on définit l’application $ p(x) = x \mod 1 $.

Que signifie cette notation ? De manière intuitive : à chaque réel $x$, on associe uniquement sa partie décimale - c’est-à-dire ce qui suit la virgule - afin de le représenter sur le cercle.

Par exemple, si $ x = 1{,}3 $, sa partie décimale est 0,3 ; on place donc ce point à l’endroit du cercle correspondant à 0,3. Si $ x = 2{,}7 $, la partie décimale est 0,7, ce qui correspond au même point que $0{,}7$.
enroulement de la droite réelle sur un cercle

On remarque qu’à chaque fois que $x$ augmente d’une unité (par exemple de 1,3 à 2,3 puis 3,3), son image reste inchangée sur le cercle.

Ce procédé d’« enroulement » revient à identifier les points 0 et 1, ainsi que tous ceux qui leur sont congrus modulo 1.

Étudions maintenant quelques cas concrets d’intervalles.

Intervalle (0,1) dans $ \mathbb{R} $
L’intervalle $ (0, 1) $ s’enroule pour former un arc de cercle ouvert, sans inclure le point 0. Il reste ouvert dans l’espace quotient, car sa préimage dans $ \mathbb{R} $ est elle aussi un ouvert.
Intervalle (1,2) dans $ \mathbb{R} $
L’intervalle $ (1,2) $ se projette exactement sur le même arc que $ (0,1) $, car $1 \mod 1 = 0$ et $2 \mod 1 = 0$. Il n’apporte donc aucune information nouvelle à la topologie quotient.
Intervalle (0,2) dans $ \mathbb{R} $
L’intervalle $ (0,2) $ couvre toute la circonférence, en passant deux fois par chaque point. Bien qu’il soit ouvert dans $ \mathbb{R} $, son image sur le cercle correspond à l’ensemble tout entier, qui est ici à la fois ouvert et fermé (clopen), puisque le cercle ne possède pas de bord.

Remarque : Cet exemple illustre que l’image d’un ouvert de $ \mathbb{R} $ n’est pas nécessairement un ouvert dans l’espace quotient.

En revanche, tout ouvert du cercle possède toujours une préimage ouverte dans $ \mathbb{R} $.

En effet, « dérouler » un ouvert du cercle vers $ \mathbb{R} $ donne une union (infinie) d’intervalles ouverts.

Cependant, la réciproque n’est pas garantie : un ouvert de $ \mathbb{R} $ n’a pas forcément une image ouverte sur le cercle.

Conclusion

On ne peut donc pas supposer qu’un ouvert de $ \mathbb{R} $ se projette automatiquement en un ouvert du cercle, car l’application de projection peut modifier la structure topologique de l’ensemble.

Exemple 3

Dans ce troisième exemple, nous construisons une topologie quotient à partir d’une suite finie d’entiers consécutifs, en identifiant le premier ($m$) et le dernier ($n$) éléments de la séquence $ \{ m, m+1, \ldots, n \} \subset \mathbb{Z} $.

Considérons la suite des sept entiers consécutifs de 1 à 7 :

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

Ce sous-ensemble forme un intervalle numérique, puisqu’il est constitué d’entiers successifs.

Nous identifions maintenant le premier élément (1) avec le dernier (7), comme si nous refermions une ligne droite pour former une boucle ou un cercle.

création d’un cercle numérique à partir d’un intervalle

On obtient alors une structure appelée cercle numérique $ C_6 $, composée de 6 points reliés en anneau.

Dans ce cercle, chaque point est adjacent à exactement deux voisins, selon une disposition cyclique.

Il s’agit bien d’un cas de topologie quotient, car la structure initiale a été transformée en un nouvel espace topologique par identification de points.

Remarque : Ce résultat est analogue à celui obtenu en identifiant les extrémités d’un intervalle réel $(a,b)$, mais ici nous travaillons avec des entiers, ce qui produit un ensemble discret et fini.

Le cercle numérique constitue également un exemple de topologie numérique, où chaque point est relié à ses voisins immédiats selon une relation de proximité définie.

Il s’agit d’un espace discret, dans lequel on applique des concepts comme la connexité et les ouverts numériques.

Remarque : En topologie numérique, un ensemble $ U $ est dit ouvert si, pour tout point $ x \in U $, ses voisins (au sens de la connexité choisie) appartiennent aussi à $ U $ - connexité-2 en 1D, connexité-4 ou -8 en 2D, connexité-6 ou -18 en 3D.

Il est important de noter que la topologie quotient et la topologie numérique relèvent de cadres conceptuels distincts.

En d’autres termes, bien que le cercle numérique puisse résulter d’une identification de points, il appartient à une autre catégorie au sein de la topologie discrète.

Exemple 4

Considérons l’ensemble des réels $ \mathbb{R} $, muni de sa topologie usuelle, et définissons une application quotient $ p : \mathbb{R} \to \{a, b, c\} $ comme suit :

$$ p(x) = \begin{cases} a \quad \text{si} \quad x < 0 \\ \\ b \quad \text{si} \quad x = 0 \\ \\ c \quad \text{si} \quad x > 0 \\ \end{cases} $$

Autrement dit, cette application contracte l’ensemble des réels strictement négatifs en un unique point $ a $, envoie le point $ 0 $ sur $ b $, et regroupe les réels strictement positifs en un point $ c $.

La topologie quotient induite par $ p $ est déterminée par les préimages de ces trois points.

On observe les préimages suivantes :

$ p^{-1}(a) = (-\infty, 0) $, un ouvert de $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, qui n’est pas ouvert dans $ \mathbb{R} $,
$ p^{-1}(c) = (0, \infty) $, également ouvert dans $ \mathbb{R} $.

Dans une topologie quotient, un sous-ensemble de $ \{a, b, c\} $ est ouvert si, et seulement si, sa préimage par $ p $ est un ouvert de $ \mathbb{R} $. Il en résulte que sont ouverts dans cette topologie :

Le singleton $ \{a\} $, puisque $ p^{-1}(\{a\}) = (-\infty, 0) $ est ouvert,
Le singleton $ \{c\} $, car $ p^{-1}(\{c\}) = (0, \infty) $ est ouvert,
L’union $ \{a, c\} $, dont la préimage est $ \mathbb{R} \setminus \{0\} $, également ouverte.

Par ailleurs, les ensembles $ \emptyset $ et $ \{a, b, c\} $ sont toujours ouverts dans toute topologie, y compris la topologie quotient :

L’ensemble total $ \{a, b, c\} $ est ouvert car $ p^{-1}(\{a, b, c\}) = \mathbb{R} $, ouvert dans sa topologie usuelle,
L’ensemble vide $ \emptyset $ est ouvert car $ p^{-1}(\emptyset) = \emptyset $, qui est toujours ouvert.

En revanche, le singleton $ \{b\} $ n’est pas ouvert dans la topologie quotient, car sa préimage $ \{0\} $ n’est pas un ouvert de $ \mathbb{R} $.

En conclusion, les seuls ouverts de la topologie quotient sur $ \{a, b, c\} $ sont $ \emptyset $, $ \{a\} $, $ \{c\} $, $ \{a, c\} $ et $ \{a, b, c\} $. Le point $ b $, correspondant à 0, ne peut être contenu dans aucun ouvert propre non trivial, car il ne possède aucun voisinage ouvert dans l’espace d’origine.

Autrement dit, $ b $ agit comme une singularité topologique : un point isolé qui interrompt la continuité locale de la structure.

Propriétés de la topologie quotient

Rappelons maintenant quelques propriétés fondamentales de toute topologie quotient :

Les ensembles vide et total sont toujours ouverts
Dans toute topologie quotient, $ \emptyset $ et l’ensemble total $ A $ sont par définition ouverts.
- Préimage de l’ensemble vide
  $ p^{-1}(\emptyset) = \emptyset $ est ouvert dans tout espace topologique, donc $ \emptyset $ est ouvert dans $ A $.
- Préimage de l’ensemble total
  $ p^{-1}(A) = X $, qui est ouvert dans $ X $ puisque c’est l’ensemble total.
Remarque : Cela confirme que les ensembles triviaux - le vide et le total - conservent toujours leur statut d’ouverts, y compris dans les topologies induites.
Unions arbitraires d’ouverts
Si chaque $ U_i $ est ouvert dans $ A $, alors leur réunion est également un ouvert :
$$ \left( \forall i,\ U_i \text{ ouvert dans } A \right) \Rightarrow p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) \text{ est ouvert dans } X. $$
Remarque : Comme l’union de n’importe quel nombre d’ouverts reste un ouvert dans $ X $, cette propriété est automatiquement transmise à la topologie quotient.
Intersections finies d’ouverts
Si les $ U_i $ sont ouverts dans $ A $, alors leur intersection finie est également un ouvert de $ A $, car
$$ p^{-1}\left( \bigcap U_i \right) = \bigcap p^{-1}(U_i) \text{ est ouvert dans } X. $$
Remarque : La stabilité des ouverts par intersection finie dans $ X $ garantit que cette propriété se reflète fidèlement dans la topologie quotient.

Ces propriétés constituent les piliers fondamentaux permettant de comprendre la structure et le comportement des espaces topologiques quotients.