Continuité en topologie

Soient $X$ et $Y$ deux espaces topologiques. Une application $f : X \to Y$ est dite continue si, pour tout ouvert $V$ de $Y$, l’image réciproque $f^{-1}(V)$ est un ouvert de $X$.

Autrement dit, une fonction continue en topologie « respecte » la structure des ouverts lorsqu’elle fait passer les points d’un espace à un autre.

La continuité topologique vise à préserver la cohérence de la structure ouverte d’un espace à l’autre.

Remarque : En topologie, la notion de continuité est plus générale que celle de l’analyse classique, où elle repose sur la distance entre les points. En analyse, la continuité exprime la proximité des points ; en topologie, elle s’intéresse à la manière dont une fonction interagit avec les ouverts. En ce sens, la définition topologique permet d’évaluer si une fonction « respecte » la structure des ouverts, même dans des contextes où la notion de distance n’a aucun sens.

Par exemple, on peut modéliser par une fonction continue le fait de « déformer » une figure géométrique sans la déchirer ni la couper.

La continuité assure ainsi que la structure initiale - notamment les ensembles ouverts - demeure intacte après transformation.

Un exemple concret
Théorème de la base pour la continuité
Continuité dans les topologies plus grossières et plus fines
Connexité et continuité : deux notions fondamentales de la topologie
Remarques

Un exemple concret

Considérons deux espaces topologiques $X = \{a, b, c, d\}$ et $Y = \{1, 2\}$.

Les ouverts de $X$ sont : $\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}$.
Les ouverts de $Y$ sont : $\{\}, \{1\}, \{1, 2\}$.

Définissons une fonction $f : X \rightarrow Y$ de la façon suivante :

$ f(a) = 1 $, $ f(b) = 1 $, $ f(c) = 2 $, $ f(d) = 2 $

La fonction est-elle continue au sens de la définition topologique ?

Pour le déterminer, représentons graphiquement la fonction $f$ et les deux espaces topologiques, en mettant en évidence les ouverts dans chacun.

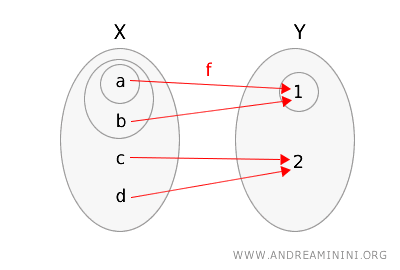
un exemple de continuité topologique

Vérifions maintenant si la définition est satisfaite :

Considérons l’ouvert $\{1\}$ de $Y$ ; son image réciproque est $ f^{-1}(\{1\}) = \{a, b\} $, qui est un ouvert de $X$.
Considérons l’ouvert $\{1, 2\}$ de $Y$ ; son image réciproque est $ f^{-1}(\{1, 2\}) = \{a, b, c, d\} $, également ouvert dans $X$.

Il n’est pas nécessaire de considérer l’ensemble vide, qui est toujours ouvert quel que soit l’espace topologique.

En conclusion, puisque l’image réciproque de tout ouvert de $Y$ est un ouvert de $X$, la fonction $f$ est continue.

Exemple 2

Considérons maintenant une autre application $g : X \rightarrow Y$ définie comme suit :

$ g(a) = 1 $, $ g(b) = 1 $, $ g(c) = 1 $, $ g(d) = 2 $

On représente la fonction $g$ et les deux espaces topologiques en mettant en valeur les ouverts pertinents.

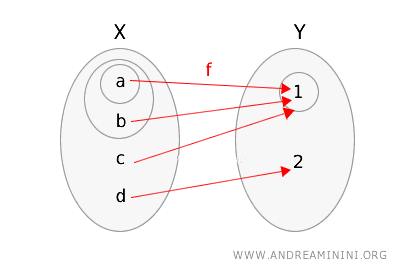
exemple de fonction non continue

Vérifions si la continuité est respectée :

L’ouvert $\{1\}$ de $Y$ a pour image réciproque $ g^{-1}(\{1\}) = \{a, b, c \} $, qui n’est pas un ouvert de $X$.

Comme il existe un ouvert de $Y$ dont l’image réciproque n’est pas ouverte dans $X$, on conclut que la fonction $g$ n’est pas continue.

Exemple 3

Examinons maintenant la fonction identité $ id : X \to X $ définie par $ id(x) = x $ pour tout $ x \in X $.

$$ x = f(x) $$

Autrement dit, la fonction identité ne modifie aucun élément de l’espace. D’un point de vue topologique, cela signifie que tout ouvert est envoyé sur lui-même, donc reste ouvert.

Par conséquent, la fonction identité $ f(x) = x $ est toujours continue, car elle ne modifie en rien la structure topologique de l’espace.

Exemple 4

Considérons enfin une fonction constante $ f : X \to Y $, définie par $ f(x) = c $ pour tout $ x \in X $.

$$ f(x) = c $$

Autrement dit, quel que soit l’élément choisi dans $X$, la fonction renvoie toujours la même valeur $c$.

D’après la définition topologique, pour que $f$ soit continue, l’image réciproque de tout ouvert de $Y$ doit être un ouvert de $X$.

Deux cas sont possibles :

Si $c \in V$, alors $ f^{-1}(V) = X $, qui est un ouvert.
Si $c \notin V$, alors $ f^{-1}(V) = \emptyset $, qui est aussi un ouvert.

Dans les deux cas, l’image réciproque est bien un ouvert de $X$.

On peut donc conclure que la fonction constante $ f(x) = c $ est continue.

Remarque : Cet exemple illustre que la continuité d’une fonction topologique dépend à la fois de sa définition propre et de la structure des espaces considérés. Dans le cas d’une fonction constante, l’image réciproque de tout ouvert de $Y$ est toujours ouverte dans $X$, ce qui garantit sa continuité.

Exemple 5

Considérons à présent l’application identité $ f : X \to Y $, définie par $ f(x) = x $, mais cette fois entre deux espaces topologiques distincts :

$X$ est l’ensemble des réels $ \mathbb{R} $, muni de la topologie usuelle, dans laquelle les ouverts sont les intervalles ouverts $ (a, b) $.
$Y$ est également $ \mathbb{R} $, mais muni de la topologie de la borne inférieure, où les ouverts sont de la forme $[a, b)$.

Pour déterminer si $f$ est continue, il suffit d’examiner si l’image réciproque de tout ouvert de $Y$ est un ouvert dans $X$.

Considérons l’ouvert $ [0, 1) $ de $Y$, qui est bien un élément de la topologie de la borne inférieure.

Comme $f$ est l’identité, on a $ f^{-1}([0, 1)) = [0, 1) $.

Or, $ [0, 1) $ n’est pas un ouvert dans la topologie usuelle.

Remarque : Dans la topologie usuelle, un ensemble est ouvert s’il existe, autour de chaque point, un intervalle entièrement contenu dans cet ensemble. Dans $ [0, 1) $, cette propriété échoue au point $0$, car tout intervalle centré en $0$ inclurait des réels négatifs.

On en conclut que l’application identité $ f : \mathbb{R} \to \mathbb{R} $, définie entre deux topologies différentes, n’est pas continue.

Cet exemple illustre clairement que la continuité d’une fonction dépend non seulement de la fonction elle-même, mais aussi des topologies sur les espaces de départ et d’arrivée.

Autrement dit, une même fonction - ici l’identité $f(x) = x$ - peut ne pas être continue si les structures topologiques varient.

Théorème de la base pour la continuité

Soient $X$ et $Y$ deux espaces topologiques. Une fonction $f : X \to Y$ est continue si, et seulement si, pour tout ensemble $B_Y$ appartenant à une base de la topologie de $Y$, l’image réciproque $f^{-1}(B_Y)$ est un ouvert dans $X$.

Ce théorème est particulièrement puissant car il simplifie considérablement la vérification de la continuité d’une application.

Au lieu d’examiner tous les ouverts de $Y$, il suffit d’étudier un ensemble réduit : les éléments d’une base de la topologie de $Y$.

On réduit ainsi drastiquement le nombre de cas à vérifier, ce qui rend l’analyse plus rapide et plus efficace.

Démonstration : Tout ouvert de $Y$ peut s’écrire comme une union (éventuellement infinie) d’éléments de sa base $B_Y$. Si l’image réciproque de chaque élément de la base est un ouvert de $X$, alors l’image réciproque de toute union (comme union d’ouverts) est elle aussi ouverte dans $X$. On en déduit que $f$ est continue.

Exemple

Soient $X = \{a, b, c, d\}$ et $Y = \{x, y, z\}$, munis des topologies suivantes :

La topologie de $X$ est $ \tau_X = \{\emptyset, \{a\}, \{a, b\}, \{a, b, c, d\}\} $.
La base de la topologie de $Y$ est $B_Y = \{\{x\}, \{y\}, \{z\}\}$.

Les ensembles ouverts de $Y$ sont formés par unions d’éléments de cette base. Par exemple :

Les ensembles $ \{x, y\} $, $ \{x, z\} $, $ \{y, z\} $, et $ \{x, y, z\} $ ne figurent pas dans la base, mais sont bien ouverts car unions d’éléments de celle-ci.

Définissons maintenant une fonction $f : X \to Y$ par :

$f(a) = x$
$f(b) = x$
$f(c) = y$
$f(d) = z$

Pour déterminer si $f$ est continue, examinons les préimages des ensembles de la base $B_Y$.

$f^{-1}(\{x\}) = \{a, b\}$, qui est un ouvert de $X$.
$f^{-1}(\{y\}) = \{c\}$, qui n’est pas ouvert dans $X$, puisque $ \{c\} \notin \tau_X $.

Puisqu’il existe un ensemble de base dont l’image réciproque n’est pas ouverte dans $X$, on conclut que la fonction $f$ n’est pas continue.

Remarque : Il suffit d’un seul contre-exemple - c’est-à-dire un élément de la base dont la préimage n’est pas ouverte - pour conclure à la discontinuité d’une fonction. Il n’est pas nécessaire d’examiner les autres cas.

Continuité dans les topologies plus grossières et plus fines

Si une fonction est continue pour une topologie plus grossière, alors elle l’est également pour toute topologie plus fine définie sur le même ensemble.

En revanche, la réciproque ne s’applique pas en général : une fonction peut être continue dans une topologie plus fine sans l’être dans une topologie plus grossière.

Différence entre topologies plus fine et plus grossière. Soient deux topologies sur un même ensemble $X$. On dit que l’une est plus grossière si elle contient moins d’ouverts, et plus fine si elle en contient davantage.

Exemple

Considérons l’ensemble $X = \{a, b\}$, muni de deux topologies distinctes :

Topologie plus grossière : $ \tau_1 = \{\varnothing, \{a, b\}\} $, où seuls l’ensemble vide et l’ensemble total sont ouverts.
Topologie plus fine : $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $, où les singletons $\{a\}$ et $\{b\}$ sont également considérés comme ouverts.

Définissons une fonction $f : X \to Y$, avec $Y = \{1\}$, de la manière suivante :

$$ f(a) = 1 \quad ; \quad f(b) = 1 $$

Dans la topologie $ \tau_1 $, les seuls ouverts sont $ \varnothing $ et $ \{a, b\} $.

Vérifions si $f$ est continue :

$ f^{-1}(\varnothing) = \varnothing $, qui est ouvert dans $ \tau_1 $.
$ f^{-1}(\{1\}) = \{a, b\} $, également ouvert dans $ \tau_1 $.

On en conclut que la fonction $f$ est continue pour la topologie grossière $ \tau_1 $.

Comme tout ouvert de $ \tau_1 $ est aussi un ouvert de $ \tau_2 $, il s’ensuit que $f$ est également continue pour la topologie plus fine $ \tau_2 $.

Dans $ \tau_2 $, les ouverts sont $ \varnothing $, $ \{a\} $, $ \{b\} $ et $ \{a, b\} $.

$ f^{-1}(\varnothing) = \varnothing $, ouvert dans $ \tau_2 $.
$ f^{-1}(\{1\}) = \{a, b\} $, ouvert dans $ \tau_2 $.

Ainsi, la fonction $f$ est continue dans les deux topologies.

Mais la réciproque n’est pas toujours vérifiée : une fonction peut être continue dans une topologie plus fine, tout en cessant de l’être dans une topologie plus grossière, en raison du plus petit nombre d’ouverts disponibles dans cette dernière.

Exemple 2

Considérons à nouveau l’ensemble $X = \{a, b\}$, muni des mêmes topologies :

Topologie plus grossière : $ \tau_1 = \{\varnothing, \{a, b\}\} $
Topologie plus fine : $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $

Définissons maintenant une fonction $g : X \to Y$, avec $Y = \{1, 2\}$, comme suit :

$$ g(a) = 1 \quad ; \quad g(b) = 2 $$

La fonction $g$ est continue dans la topologie plus fine $ \tau_2 $, car toutes les préimages des ouverts de $Y$ y sont ouvertes :

$ g^{-1}(\varnothing) = \varnothing $, ouvert dans $ \tau_2 $.
$ g^{-1}(\{1,2\}) = \{a,b\} $, ouvert dans $ \tau_2 $.
$ g^{-1}(\{1\}) = \{a\} $, ouvert dans $ \tau_2 $.
$ g^{-1}(\{2\}) = \{b\} $, ouvert dans $ \tau_2 $.

En revanche, la fonction $g$ n’est pas continue dans la topologie grossière $ \tau_1 $, car certaines préimages ne sont pas ouvertes dans $ \tau_1 $ :

$ g^{-1}(\varnothing) = \varnothing $, ouvert dans $ \tau_1 $.
$ g^{-1}(\{1,2\}) = \{a,b\} $, ouvert dans $ \tau_1 $.
$ g^{-1}(\{1\}) = \{a\} $, qui n’est pas ouvert dans $ \tau_1 $.

On en déduit que $g$ est continue dans $ \tau_2 $, mais non dans $ \tau_1 $.

Connexité et continuité : deux notions fondamentales de la topologie

En topologie générale, la connexité et la continuité sont deux concepts centraux. Tous deux décrivent la manière dont les points d'un espace topologique sont liés, mais ils appartiennent à des registres différents : l'un concerne la structure interne de l'espace, l'autre le comportement des applications entre espaces.

Distinguer clairement ces notions est essentiel pour comprendre la logique des espaces topologiques et leurs transformations.

La connexité : une propriété intrinsèque de l'espace
Un espace topologique $ X $ est dit connexe s'il n'existe pas deux ensembles ouverts non vides, disjoints, dont la réunion soit $ X $. De manière équivalente, il est connexe s'il ne peut pas être exprimé comme l'union de deux ensembles disjoints qui soient simultanément ouverts et fermés (clopens). Intuitivement, un espace connexe ne peut pas être "scindé" en plusieurs composantes séparées sans rompre sa continuité topologique. La connexité est donc une propriété structurelle propre à l'espace, indépendante de toute application définie sur celui-ci.
La continuité : une propriété des applications
La continuité concerne une application $ f: X \to Y $ entre deux espaces topologiques. On dit que $ f $ est continue si, pour tout ensemble ouvert $ V \subseteq Y $, l'image réciproque $ f^{-1}(V) $ est un ensemble ouvert de $ X $. En d'autres termes, une application continue préserve la structure topologique du domaine : elle ne crée ni discontinuités ni ruptures dans la correspondance entre les points. Par exemple, la fonction $ f(x) = x^2 $ est continue de $ \mathbb{R} $ vers $ \mathbb{R} $ pour la topologie usuelle, mais ce fait n'implique rien quant à la connexité de $ \mathbb{R} $ lui-même.

Bien que des théorèmes établissent des liens entre ces deux notions, elles relèvent de niveaux conceptuels différents. L'une décrit une propriété de l'espace, l'autre une propriété d'une fonction définie entre espaces.

Un résultat classique illustre cette relation : si $ X $ est connexe et si $ f: X \to Y $ est continue, alors l'image $ f(X) $ est un sous-ensemble connexe de $ Y $. Ainsi, la continuité préserve la connexité.

En résumé, la connexité caractérise la structure globale d'un espace topologique, tandis que la continuité décrit la régularité des applications qui opèrent sur cette structure. Ces deux notions forment les bases de la topologie moderne et de l'analyse des transformations continues.

Remarques

Quelques compléments utiles concernant la continuité en topologie :

Une fonction continue n’est pas nécessairement ouverte
Une fonction continue ne transforme pas forcément des ouverts en ouverts. Ainsi, la continuité n’implique pas que l’image d’un ouvert soit un ouvert.
Lemme du recollement
Si deux fonctions continues $ f : A \to Y $ et $ g : B \to Y $ coïncident sur $ A \cap B $, alors il est possible de définir une fonction $ h : A \cup B \to Y $ continue, qui prolonge $f$ et $g$.
Continuité de l’inclusion
L’application inclusion $ f : Y \to X $, définie par $ f(y) = y $, est toujours continue lorsqu’on considère $Y$ comme un sous-espace topologique de $X$.
Continuité dans la topologie quotient
Si $f : X \to A$ est surjective, on munit $A$ de la topologie quotient afin de rendre $f$ continue.
Théorème sur l’adhérence
Si $x \in \overline{A}$ dans $X$, alors $f(x) \in \overline{f(A)}$ dans $Y$, à condition que $f$ soit continue.
Définition par les ouverts
Une fonction $f$ est continue si, et seulement si, l’image réciproque de tout ouvert de $Y$ est un ouvert dans $X$.
Définition par les fermés
De manière équivalente, $f : X \to Y$ est continue si la préimage de tout fermé de $Y$ est un fermé dans $X$.
Composition de fonctions continues
La composition $ g \circ f $ de deux fonctions continues est elle aussi continue.
Continuité et suites convergentes
Si $f : X \to Y$ est continue, alors l’image d’une suite convergente dans $X$ converge vers l’image de la limite dans $Y$.
Fonctions polynomiales
Dans $ \mathbb{R} $ muni de la topologie usuelle, toute fonction polynomiale $ p(x) = a_nx^n + \dots + a_0 $ est continue.

Et bien d’autres propriétés encore…